在物理学中,紧緻(compactification),又称紧緻化,指改变时空中某些维度的拓扑结构,使其从展开的无限大尺度,变成有限大的周期性结构。紧化在弦理论中用于解决多维空间的额外空间问题。
基本介绍
- 中文名:紧化
- 外文名:compactification
- 又称:紧緻化
- 学科:物理学
- 套用:弦理论
历史
在弦理论中,将超弦理论放置在10 维中就会没有反常,没有反常是个非常重要同时令人满怀憧憬的发现维数确定以后的问题是额外维的问题,即这10 维中超出人类所能理解的那6维如何解决。
20 世纪20 年代最早曾经被卡鲁查( Th.Kaluza)和克莱因( O.Klein)提出过, 就是将其看做是捲起来了, 卷到了极小不能被看到的尺度。这种将维度卷到了非常小以至于很难被看到的程度的思想被称为紧化。
简介
场论中的紧緻化
卡鲁扎-克莱因理论是一个紧化的例子。通过把额外的第五维捲曲成一个半径非常小的圆,引力和电磁力得以被统一理解。在超引力的领域中,11维超引力中捲曲的7维流形的对称性,用来在引力框架内包容描述强力、弱力和电磁力的标準模型。
弦论中的紧緻化
弦论中的紧緻化,是卡鲁扎-克莱因理论的一种扩充和套用。考虑费米子自由度后,超弦理论只有在10维才自洽。为了联繫10维的超弦理论和4维的现实世界,我们通常把多余的6维捲曲起来。为了保证4维有效理论至少具有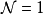 超对称,6维流形的完整群应为
超对称,6维流形的完整群应为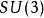 而非最广泛的情形
而非最广泛的情形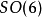 ,因此6维流形应是卡拉比–丘流形,包含轨形、不可定向形或D膜的紧緻化亦被广泛讨论。
,因此6维流形应是卡拉比–丘流形,包含轨形、不可定向形或D膜的紧緻化亦被广泛讨论。
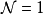
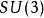
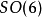
不同的额外维流形的模对应于4维有效场论中不同的真空。为了固定这些模,与D膜的耦合规範场被用来确定低维有效理论的势。这即为通常所说的通量紧化。由于卡拉比–丘流形的贝蒂数 和
和 通常很大,其通量紧緻化的合理真空数量惊人;这一性质被用来解释理论计算的宇宙学常数和观测所得的暗能量不符合的疑难。
通常很大,其通量紧緻化的合理真空数量惊人;这一性质被用来解释理论计算的宇宙学常数和观测所得的暗能量不符合的疑难。


扩展:紧化(数学)
在数学中,紧化是将一个拓扑空间扩大为紧的过程或结果。紧化的方法有多种,但每一种方法都是以某种方式添加“无穷远点”控制“跑向无穷远”的点或阻止这样的“逃逸”。
拓扑空间 作为稠密子集嵌入一个紧空间称为
作为稠密子集嵌入一个紧空间称为 的一个紧化。将拓扑空间嵌入紧空间中经常有用,因为紧空间有一些特殊性质。嵌入紧豪斯多夫空间可能特别让人感兴趣。因为每个紧豪斯多夫空间是一个吉洪诺夫空间,而吉洪诺夫空间的每个子空间是吉洪诺夫的,我们得出每个有豪斯多夫紧化的空间必须是吉洪诺夫空间。事实上,其逆亦真;吉洪诺夫空间是存在豪斯多夫紧化的充分必要条件。
的一个紧化。将拓扑空间嵌入紧空间中经常有用,因为紧空间有一些特殊性质。嵌入紧豪斯多夫空间可能特别让人感兴趣。因为每个紧豪斯多夫空间是一个吉洪诺夫空间,而吉洪诺夫空间的每个子空间是吉洪诺夫的,我们得出每个有豪斯多夫紧化的空间必须是吉洪诺夫空间。事实上,其逆亦真;吉洪诺夫空间是存在豪斯多夫紧化的充分必要条件。


很多有趣的非紧空间确实有特别类型的紧化,这个事实使紧化成为拓扑学中的常用技巧。
亚历山德罗夫单点紧化
对一个拓扑空间 ,它的(亚历山德罗夫)单点紧化
,它的(亚历山德罗夫)单点紧化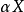 是通过添加额外一点
是通过添加额外一点 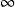 (通常叫做无穷远点)得到的,定义新空间的开集是
(通常叫做无穷远点)得到的,定义新空间的开集是 中的开集以及具有
中的开集以及具有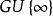 形式的集合,这里
形式的集合,这里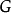 是
是 的一个子集使得
的一个子集使得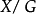 闭且紧。
闭且紧。 的单点紧化是豪斯多夫的若且唯若
的单点紧化是豪斯多夫的若且唯若 是豪斯多夫的且局部紧。
是豪斯多夫的且局部紧。

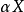
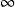

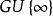
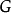

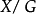


斯通-切赫紧化
其次,豪斯多夫紧化,即紧化中紧空间是豪斯多夫。一个拓扑空间有豪斯多夫紧化若且唯若它是吉洪诺夫。在这种情形,存在惟一(差一个同胚)“最一般的”豪斯多夫紧化, 的斯通-切赫紧化,记作
的斯通-切赫紧化,记作 。空间
。空间 由泛性质刻画,任何从
由泛性质刻画,任何从 到一个紧豪斯多夫空间
到一个紧豪斯多夫空间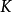 的连续函式可以惟一地延拓为从
的连续函式可以惟一地延拓为从 到
到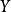 的连续函式。更确切地说,
的连续函式。更确切地说,  是一个包含
是一个包含 的紧豪斯多夫空间使得
的紧豪斯多夫空间使得 上由
上由  诱导的拓扑与
诱导的拓扑与 上本来的拓扑相同,且对任何连续映射
上本来的拓扑相同,且对任何连续映射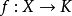 ,这里
,这里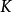 是一个紧豪斯多夫空间,存在惟一连续映射
是一个紧豪斯多夫空间,存在惟一连续映射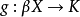 使得
使得 限制在
限制在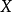 上等同于
上等同于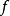 。
。




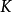

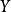





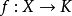
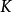
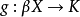

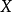
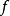
斯通-切赫紧化可具体地构造如下:设 是从
是从 到闭区间
到闭区间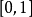 的连续函式集合。则
的连续函式集合。则 中每一点可与
中每一点可与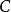 上一个取值函式等同。这样
上一个取值函式等同。这样 可与
可与 的一个子集等价,这里
的一个子集等价,这里 是从
是从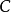 到
到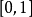 的所有函式集合。由吉洪诺夫定理后者是紧的,
的所有函式集合。由吉洪诺夫定理后者是紧的, 的闭包作为该空间子集也是紧的。这就是斯通-切赫紧化。
的闭包作为该空间子集也是紧的。这就是斯通-切赫紧化。


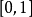

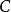



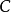
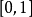

相关术语
- 弦理论
- 超弦理论
- 卡拉比–丘流形
- 卡鲁扎-克莱因理论
