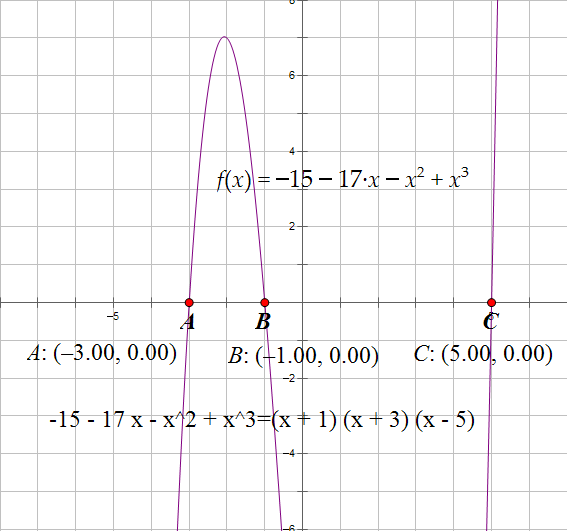
主元法

主元法的利用

1.因式分解(ab+bc+ca)(a+b+c)-abc.

分析：如果懂得因式定理的话，解此题自然会流畅很多，但是用主元法的话，也十分简便。

拆开原式,并按a的降幂排列得：

(b+c)a^2+(b^2+c^2+2bc)a+b(bc+c^2)

=(a+c)(b+c)(a+b)------------------------------【十字相乘法】

十字相乘图为

a--------------- b

(b+c)a -----bc+c^2

对于低次因式分解，主元法与十字相乘法的配合是卓有成效的。

2.因式分解16y+2x^2(y+1)^2+(y-1)^2x^4

分析：本题尚且属于简单例用，只是稍加难度，以y为主元会使原式极其烦琐，而以x为主元的话，原式的难度就大大降低了。

原式=(y-1)^2x^4+2(y+1)^2x^2+16y---------------------【主元法】

=(x^2y^2-2x^2y+x^2+8y)(x^2+2)---------------------【十字相乘法】

十字相乘图为

(y-1)^2x^2 ----8y

x^2------------2

如果能很好地利用主元法，低次因式分解就不会太难了。

1.因式分解2x^3+6y^3+15z^3-9x^2y+7xy^2-x^2z-16xz^2-37y^2z+32yz^2+13xyz

分析：本题属于高难度因式分解中的中档题，如果不假思索就上边的方法，就会处处碰壁。

1.原式=2x^3-(9y+z)x^2+(13yz+7y^2-16z^2)x+6y^3+15z^3-37y^2z+32yz^2---------------【主元法】

这样本题的条理就清晰多了，现抛开x,只看6y^3+15z^3-37y^2z+32yz^2,

这是一个2元三次因式分解，难度简单多了。

原式=6y^3-9zy^2-(28y^2z-32yz^2-15z^3)-------------------------【拆项法】

=(2y-3z)(y-5z)(3y+z)

再代入原题目，接下来的工作就简单了。

由于首项x係数为2，所以本题难度综合来讲不是太难，算出係数2是与(y-5z)结合的。

所以原式=(x-2y+3z)(2x+y-5z)(x-3y-z)------------------------【拆项法及十字相乘法】

竞赛类的学生，因式分解的高手可以演算一下,这是个很好的练习,对你们会很有帮助。