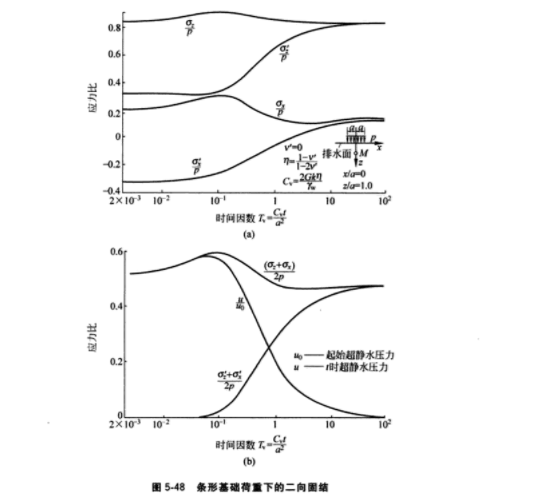
用比奥理论解饱和土的固结问题时出现一种异乎寻常的现象：在不变的荷重施加于土体上以后的某段时间，土体内的孔隙水压力不是下降，而是继续上升，而且超过应有的压力值。该现象先后由曼代尔和克雷尔发现，故称曼代尔－克雷尔效应，或称为应力传递效应。产生曼代尔－克雷尔效应的原因可以解释如下。在表面透水的地基面上施加荷重，经过短暂的时间，靠近排水面的土体由于排水发生体积收缩，应力与有效应力均有增加。土的泊松比也随之改变。但是内部土体还来不及排水，为了保持变形协调，表层土的压缩必然挤压土体内部，使那里的应力有所增大。因此，某个区域内的总应力分量将超过它们的起始值，而内部孔隙水由于收缩力的压迫，其压力降上升。水平总应力分量的相对增长（与起始值相比）比垂直分量的相对增长要大。浅部土层距离排水面较近，超孔压消散较快，深部土层超孔压消散缓慢，并产生了曼代尔-克雷尔效应。

按平面应变问题分析，该效应有以下特点：地面排水性能愈差，该效应愈不显着，地面不透水时，几乎无该效应。如果地面透水，超静水压力出现峰值点的时间随深度而推后，并且峰值愈来愈高。由于曼代尔－克雷尔效应，地面透水的土体中一点的剪应力随时间变化，最大值可能在固结过程中的基础边缘产生。

太沙基固结理论只在一维情况下是精确地，对二维、三维问题并不精确。比奥（Biot）从较严格的固结机理出发推导了準确反映孔隙压力消散与土骨架变形相互关係的三维固结方程，一般称为真三维固结理论，而将太沙基三维方程称为拟三维固结方程。比奥(M.A.Biot)于1941年创立的三维固结理 论。该理论将弹性理论求解土体的应力和变形的方 法与渗透水流连续条件相结合，建立由四个偏微分 方程所组成的固结方程组，可同时求解土体在固结 过程中任意点的孔隙水压力和变形。常称为真固结 理论。其求解非常複杂，一般需用数值法并藉助于电子计算机。太沙基－伦杜列克扩散方程，又称太沙基－伦杜列克固结理论，该理论与太沙基一维固结理论建立在同一个理论基础上，即在饱和粘土的固结过程中，土中任意单元体的体积变化率与流经单元体表面的水量变化率相等。在其推导过程中，只考虑了水流连续条件和弹性的应力应变关係，而没有涉及土体变形的几何条件，这种理论又被称为準多维固结理论。可以利用差分法求解。

由外荷载引起的孔隙水压应力，称为超静孔隙水压应力。超静孔隙水压应力将会随着时间而消散，所以超静孔隙水压应力是时间的函式。超静孔隙水压应力称为附加孔隙水压应力更为合适，在载入瞬时为最大，当固结度达到100%时为零。超静孔隙水压应力是由土体的体积变化趋势引起的，也就是说，超静孔隙水压应力是土的体积变形性质在不排水条件下的表现。这意味着土体的体积变形性质（压缩性和剪胀性）在不同的排水条件下有不同的表现。它在排水情况下表现为体积变化，而在不排水条件下则表现为超静孔隙水压应力变化。

超静孔隙水压力(excess pore water pressure)是由土的变形趋势引起的孔隙水压力，也就是说，土体本应发生应变，但由于一时排水受阻，土中产生孔隙水压力，使作用于土骨架上的有效应力发生变化，从而限制其变形。超静孔隙水压力往往伴随着渗流和固结。超静孔隙水压力是由于外部作用或者边界条件变化在土体中引起的不同于静孔隙水压力的那部分孔隙水压力，在有排水条件下，它将逐渐消散，并在消散过程中伴随土体的体积变化。