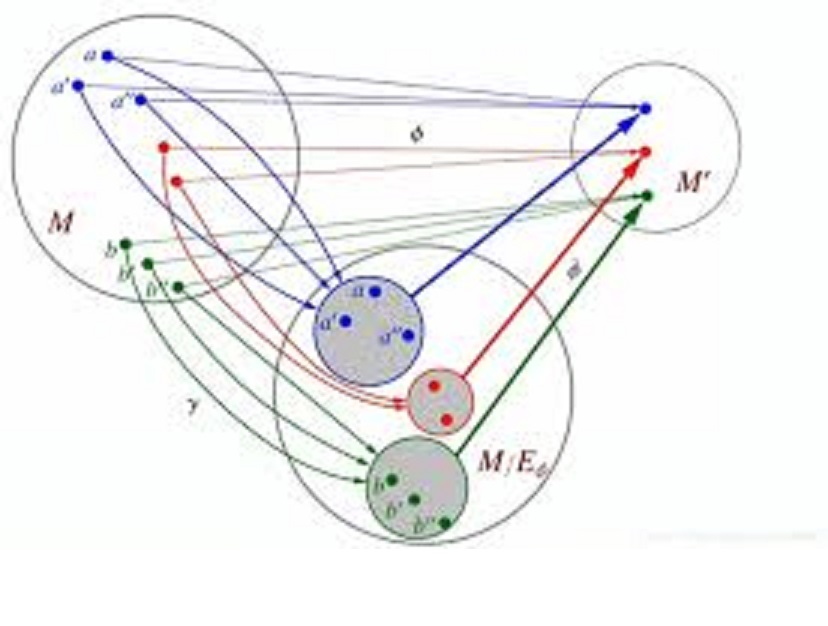
在数学和计算机科学中,半自动机或M-act是幺半群在集合上的乘法性运算。从代数结构的观点来看,它非常接近于群作用的概念。从计算机科学的观点来看,它是只有输入没有输出的自动机。从範畴论的观点来看,作用是如範畴上的函子般重要。这个概念也叫做S-集合、M-集合、M-运算元、S-系统、S-自动机、转移系统、运算元幺半群、变换半群或转移幺半群。本文力图表现出它们表示的是同一个概念,儘管在使用中有各种概念和术语的变体。
基本介绍
- 中文名:半自动机
- 外文名:Semi-automatic machine
- 作用:幺半群在集合上的乘法性运算
简介
半自动机是三元组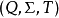 ,这里的
,这里的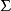 是叫做“输入字母表”的非空集合,Q是叫做“状态集合”的非空集合,而T是“转移函式”,
是叫做“输入字母表”的非空集合,Q是叫做“状态集合”的非空集合,而T是“转移函式”,
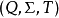
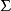
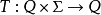
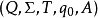
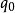
幺半群理论的一个主要主张是半自动机等价于act;所以对于任何act,都有一个独立的半自动机,或反过来说,对于任何半自动机,都有一个独立的act。这可以如下这样证实。
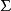
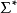

对于所有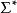 中的字w,设
中的字w,设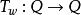 是如下递归定义的函式,对于所有Q中的q:
是如下递归定义的函式,对于所有Q中的q:
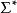
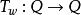

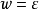
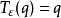
如果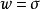 是
是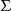 中的字母,则
中的字母,则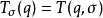 。
。
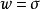
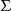
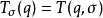
如果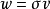 对于
对于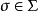 和
和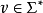 ,则
,则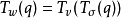 。
。
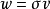
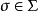
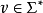
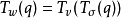
设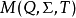 是个集合
是个集合
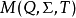
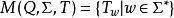
集合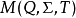 在函式複合下闭合;就是说,对于所有
在函式複合下闭合;就是说,对于所有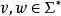 ,有着
,有着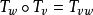 。它还包含
。它还包含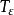 ,它是S上的恆等函式。因为函式複合根据定义是结合性的,集合
,它是S上的恆等函式。因为函式複合根据定义是结合性的,集合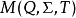 是幺半群:它叫做半自动机
是幺半群:它叫做半自动机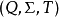 的输入幺半群、特徵幺半群、特徵半群或转移幺半群。
的输入幺半群、特徵幺半群、特徵半群或转移幺半群。
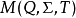
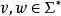
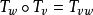
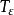
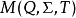
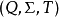
变换半群
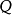
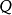

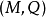
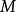
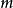


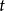
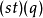
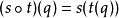
注意“半群”与“幺半群”的使用:有些作者将“半群”与“幺半群”视为同义词。然而此处一个半群不必然包含单位元素;而一个幺半群则意指含有单位元素的半群。因为作用于集合上的函式概念永远包括恆等函式概念在内,亦即施加于集合上时不做任何动作,故变换半群可藉由与恆等函式联集转为幺半群。
M-acts
设{\displaystyle M}是幺半群而{\displaystyle Q}是非空集合。如果存在一个乘法运算
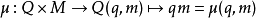
它满足性质
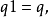
此处1表幺半群之单位元素,并且
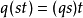
对所有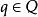 和
和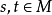 ,三元组
,三元组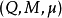 被称为右
被称为右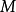 -act或简称右-act。一般而言,
-act或简称右-act。一般而言,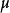 表示“
表示“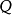 的元素与
的元素与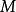 的元素的右乘法”。右-act经常写为
的元素的右乘法”。右-act经常写为 。
。
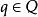
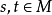
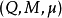
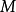
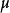
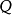
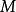

左-act定义类似,即
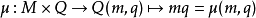
并经常表示为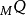 。
。
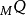
一个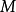 -act变换半群十分相似,然而
-act变换半群十分相似,然而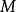 的元素本身不必然为函式,它们仅是某个幺半群的元素。所以,必须限制
的元素本身不必然为函式,它们仅是某个幺半群的元素。所以,必须限制 的作用与幺半群中的乘法一致(亦即,
的作用与幺半群中的乘法一致(亦即,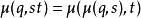 ),因为一般而言,对于某个任意
),因为一般而言,对于某个任意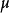 此性质可能不成立,保证此一致性可使进行函式複合时不致出问题。
此性质可能不成立,保证此一致性可使进行函式複合时不致出问题。
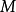
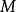

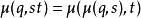
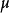
一旦加上这种限制,就可以完全放心的去掉所有括弧,因为幺半群乘积和幺半群在集合上的作用是完全满足结合性的。特别是这允许了幺半群的元素被表示为计算机科学意义上字母的字元串。这种抽象接着允许谈论一般的字元串运算,并最终导致了由字母的字元串构成的形式语言概念。
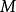
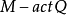
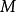
完全变换幺半群
完全变换幺半群(或完全变换半群)是所有映射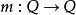 的蒐集。完全变换幺半群是自由幺半群,在允许所有可能性的意义上。完全变换幺半群的一个特殊情况是置换群。
的蒐集。完全变换幺半群是自由幺半群,在允许所有可能性的意义上。完全变换幺半群的一个特殊情况是置换群。
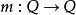
M-同态
M-同态是映射
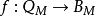
使得

对于所有 和
和 。所有M-同态的集合通常写为
。所有M-同态的集合通常写为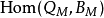 或
或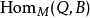 。
。


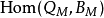
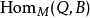
性质
如果状态集合Q是有限的,则转移函式通常表示为状态转移表。在自由群中字元串所驱动的所有可能转移的构造有一种叫de Bruijn图的图形描述。
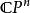
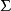
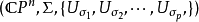
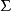

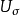
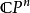
形式语言的语法幺半群同构于到接受这个语言的极小自动机的转移幺半群。
範畴Act
定义右作用的代数关係形成了一个範畴Act。对象是M-act,而範畴的态射是M-同态。