群是现代数学中最重要的具有概括性的概念之一,有关群的性质及其结构的理论称为群论。半群是群的推广。群自然是半群;反之显然未必。半群也是环的推广。
带零半群(semigroup with zero)是指含零元的半群。半群S中的元素0,若关于任意x∈S,有0x=x0=0,则称0为S的零元。
基本介绍
- 中文名:带零半群
- 外文名:semigroup with zero
- 领域:代数
- 定义:含零元的半群
- 半群:群、环的推广
- 理论:群论、环论
概念
带零半群(semigroup with zero)是指含零元的半群。半群S中的元素0,若关于任意x∈S,有0x=x0=0,则称0为S的零元。关于任意半群S,记:
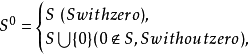
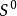
群论
群是现代数学中最重要的具有概括性的概念之一,有关群的性质及其结构的理论称为群论。
1831年,年仅20岁的青年数学家伽罗华得到n次方根可否通过对係数施行四则和开方运算来求解的判据,一举解决了五 次以上代数方程求解的千古难题。这个问 题得以解决,取决于他对置换群性质所作 的深入讨论,群的概念就在这时产生了。 现在研究代数方程的性质与群的性质之间 的关係已成为一门大理论伽罗华理论所研 究的对象,伽罗华理论在群论的发展中起 作决定性的作用。40年后克莱因的变换群 导致几何观的一次革命; 索福斯·李研究 微分方程,开创李群论,更深刻影响着数 学物理的发展。在数学物理的对称现象的 研究中,对称的概念看来是明显的,但对 对称概念的精确和一般的描述,特别是对 称性质量上的计算,却要用群论这个工具 才行。19世纪到20世纪,在几何、晶体等 物理、化学中,都弄清了对称规律的重要 意义,因此群论的方法和结果得以广泛使 用。1890年,费道洛夫用群论阐明晶体结构的几何形态,特别是20世纪30年代, 书尔、维格纳等人把群论套用于量子力学 取得成功,导致了原子、分子结构的重要 发现。现在群论已经是量子物理和量子化 学常用的工具了,这更使群论走出了纯数 学专业的数学王国,活跃于更广阔的科学 地。今天,群的概念已普遍被认为是数学 及其许多套用中最基本的概念之一,它不 但渗透到像几何学、代数拓扑学、函式论、 泛函分析及其他许多数学分支中而着重要 的作用,还形成了一些新学科,如拓扑群、 李群、代数群、算术群等。它们还具有与 群结构相联繫的其他结构,如拓扑、解析流形、代数簇等,并在结晶学、理论物理、 量子化学以至编码学、自动机理论等方面 都有重要套用。作为推广 “群” 的概念的 产物,群论及其在计算机科学中的套用, 也有很大的发展。
群的概念中有两个方面: 一是指出它的元素是哪些事物,二是元素间运算的规则,可分别用它们来研究群。研究群的元素和元素集合的各种性质,以及它们同群 的运算性质之间的联繫,这常常是研究各 种具体的群,如交换群、置换群、运动群、拓扑群等; 也可研究完全由群的运算性质 表示出来的特性,它属于抽象群论或一般 群论。下面是一些抽象群论的概念: 同构, 一个群的元素与另一个群的元素对应,运 算结果也是对应的,称两个群同构; 一个 群所含元素的个数称为群的阶,群G的阶 记为|G| ,|G|有限时为有限群,无限 时为无限群; 同构中两个群中的元素是一一对应的,若存在多对一的对应则称为同态。
半群
简单、最自然的一类代数系统。一个非空集合S连同定义在它上面的一个结合的(即满足结合律的)二元运算“·”的代数系统(S,·)称为一个半群。半群(S,·)简记为S。
半群是群的推广。群自然是半群;反之显然未必。半群也是环的推广。环在只考虑它的乘法运算的时候是一个半群,称为环的乘半群;但任何一个带零半群却未必是某个环的乘半群。半群代数理论的系统研究始于20世纪50年代(虽然,这方面的工作可追溯到1904年苏士凯维奇(Suschkwitz,A.K.)关于有限半群的论文)。在数学内部和外部的巨大推动下,半群理论已成为代数学的一个公认的分支学科,并早已以其特有的方法独立于群论和环论之外。在20世纪60年代,苏联和美国率先出版了两本专着,利雅平(Ляпин,E.C.)的《半群》和克利福德(Clifford,A.H.)与普雷斯顿(Preston,G.B.)的两卷《半群代数理论》,这对半群代数理论的发展,在国际上起了巨大的推动作用。由德国斯普林格出版社出版的《半群论坛》更是有关半群理论的一个重要的国际性专门刊物.许多数学家在世界各地开展半群理论的研究和各层次高级人才的培养(直到博士后).半群代数理论是半群理论中最基本、最活跃、也最富成果的一部分.此外,尚有半群的分析、拓扑和序理论。
设S为一个非空集合,a、b、c为它的任意元素,如果对于S所定义的一种代数运算“·”满足
(1)封闭性a·b∈s;
(2)结合律a·(b·c)=(a·b)·c。
则称S为一个半群。半群的理论在计算机、数学物理、数学语言学等方面有广泛的套用。
环论
抽象代数学的主要分支之一。它是具有两个运算的代数系.在非空集合R中定义加法“+”和乘法“·”运算,使得R中任意元a,b,c适合条件:
1.R对加法为交换群,称为R的加法群,记为(R,+);
2.R对乘法适合结合律,即(R,·)是半群,称为R的乘法半群;
3.乘法对加法的左、右分配律成立,即
a·(b+c)=a·b+a·c (左分配律),
(b+c)·a=b·a+c·a (右分配律);
则称R为结合环,简称环(通常a·b写为ab).它是环论研究的主要对象.环论起源于19世纪关于实数域的扩张与分类,以及戴德金(Dedekind,J.W.R.)、哈密顿(Hamilton,W.R.)等人对超複数系的建立和研究。韦德伯恩(Wedderburn,J.H.M.)于1907年给出的结构定理给出代数研究的模式,也成为环结构研究的模式.20世纪20-30年代,诺特(Noether,E.)建立了环的理想理论,阿廷(Artin,E.)又将代数结构定理推广到有极小条件的环.同时,对非极小条件的环,冯·诺伊曼(von Nenmann,H.)建立了正则环理论,相继盖尔范德(Гельфанд,И.М.)创立了赋值环,克鲁尔(Krull,W.)建立了局部环理论,以及哥尔迪(Goldie,A.W.)完善了极大条件环理论。
20世纪40年代,根论迅速发展,尤其是雅各布森(Jacobson,N.)于1945年引入的被称为雅各布森根的概念后,建立了本原环理论、半本原环的结构定理与本原环的稠密性定理,完善和深化了不带附加条件环的理论.20世纪50年代中期,阿密苏(Amitsur,S.A.)、库洛什(Kurosh,A.)创立了根的一般理论,环论已趋完善。
另一方面,由群表示研究的影响,产生模、群环与分次环的理论.20世纪20年代初,诺特引入了模的概念,并研究模对有限群表示的作用与环结构之间的关係,用模的语言去刻画环,特别是20世纪50年代以后,同调代数的迅速发展,使环的理论进入更高层次虽然,早在1854年,凯莱(Cayley,A.)就引入了群代数,然而,它的研究是从20世纪30年代开始直到60—70年代,受群表示论与环的理论的推动才蓬勃发展起来的.20世纪70年代后,由于分次代数的推动,群代数进入新的阶段——交叉积的研究.分次环与模发展的另一动力是交换代数几何中射影代数簇,20世纪70年代以来,由于非交换代数几何及群表示论的推动,环论已进入一个新的阶段.
若环R的乘法适合交换律,则称R为交换环.乘法半群的左(右)单位元,称为环R的左(右)单位元.乘法半群的单位元称为环R的单位元.(R,+)的零元称为环R的零元.在一个元构成的环中,零元是单位元,但两个以上的元构成的环中,零元一定不是单位元.环R的一个非空子集合S,若对R的加法、乘法也构成环,则称S是R的子环.S是R的子环若且唯若对任意a,b∈S恆有a-b∈S,ab∈S.
比结合环条件较弱的是非结合环,非结合环与代数受量子力学的刺激发展起来,但其研究的方法和思路基本上沿着结合环的格式,并早已趋完整。比结合环更弱的环类是拟环与半环,虽然早在20世纪40年代,就分别由扎森豪斯(Zassenhaus,H.)和范迪维尔(Vandiver,H.S.)提出,但它们的发展是20世纪60年代以来,受自然科学和数学其他分支(如非线性同调代数、非线性几何、泛函分析、组合数学、动力系统和计算机科学)的推动而迅速成熟起来的,现已成为环论的独立分支。
