严格凸赋范线性空间(strictly convex normed linear space)是满足严格凸性的一类赋范线性空间，简称为严格凸空间，常用于讨论最佳逼近元的唯一性，以及有界线性泛函保范延拓的唯一性等问题。内积空间是严格凸空间。
基本介绍
- 中文名：严格凸赋范线性空间
- 外文名：(strictly convex normed linear space
- 相关概念：一致凸空间
- 本质：满足严格凸性的一类赋范线性空间
- 举例：内积空间
- 学科：数学
定义
定义1 设X为赋范线性空间，如果对任何非零元x，y，当
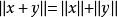
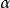
举例
（1）内积空间是严格凸空间。
（2）当p>1时，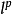
与
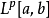均为严格凸空间。
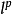
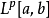
严格凸的判定
法1-利用等价条件
定理1 赋范线性空间X是严格凸的充要条件是对X中单位球面上任意两个不同的点x，y，均有
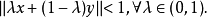
证明：（1）必要性。若不然，则存在单位球面上两个不同的点
，及
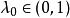，使得
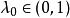
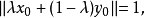
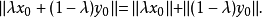
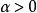
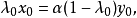
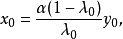
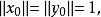
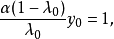
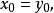
（2）充分性。若不然，则存在非零元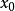
与
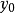，使得
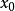
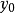
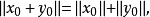
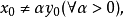
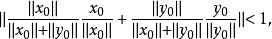
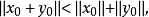
法2-利用一致凸空间
定义2 设X为赋范线性空间，如果对任何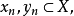
当
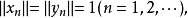且
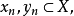
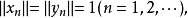
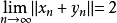
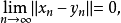
这个定义也可叙述为：如果对任何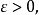
存在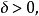
当X中的单位向量x，y满足
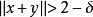时，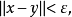
则称X为一致凸空间。
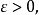
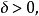
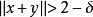
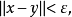
定理2 一致凸空间必是严格凸的。
证明：若一致凸空间X不是严格凸的，则必存在X中两个非零元，使得
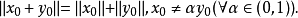
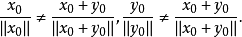
因为X是一致凸的，故而
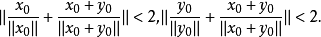
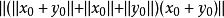
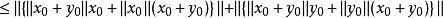
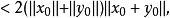
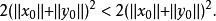
套用
赋范线性空间的严格凸性是一个重要的凸性概念，常用于讨论有界线性泛函保范延拓的唯一性问题。下面是一个重要定理。
定理3 设X为赋范线性空间，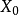
是X的一个线性子空间，
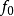是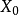上的一个连续线性泛函，如果
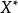是严格凸空间，则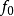在全空间X上的保范线性延拓是唯一的。反之，若X为自反空间，对任何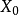和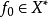
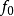，在X上的保范线性延拓是唯一的，则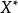必是严格凸的。
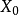
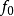
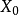
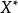
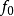
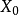
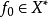
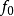
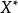
定理3的证明参见参考文献[1] 的36-37页。