全连续运算元是一类重要的有界运算元，它最接近于有限维空间上的线性运算元。设X，Y是赋范线性空间，T是X到Y的连续运算元。如果T把定义域中任何有界集映射成Y中的列紧集，则称A是全连续运算元，或紧运算元。紧运算元概念是希尔伯特(Hilbert，D.)于1906年引入的，1917年里斯(Riesz，F.)对紧运算元进行了系统的研究，1930年绍德尔(Schauder，J.P.)进一步证明了紧运算元的更多性质。

设X、Y均为赋范线性空间，T为X→Y的线性运算元，如果T将X中的任一有界集映成Y中的列紧集，则T称为全连续运算元，或紧运算元。

注：1）距离空间上的全连续运算元的定义为：设X、Y均为距离空间，T为X→Y的线性运算元，如果T将X中的任一有界集映成Y中的列紧集，则T称为紧运算元，连续的紧运算元称作全连续运算元。

显然，如果X、Y均为赋范线性空间，T为X→Y的线性运算元，那幺T是紧运算元与T是全连续运算元是等价的。

2）设X、Y均为赋范线性空间，A为X→Y的紧运算元的充要条件是对X中任何有界集，AM的闭包是Y中的紧集；这又等价于对X中任何有界点列{x_n}，{Ax_n}有在Y中收敛的子列。

设X、Y均为赋范线性空间，A为X→Y的紧运算元，则A具有以下性质：

1)运算元T为紧运算元若且唯若T将X中的闭球B(θ，1)={x： ‖x‖≤1}映成Y中的列紧集；

2)紧运算元必定是连续的；

3)设T₁、T₂为X→Y的紧运算元，α、β∈C，则αT₁+βT₂为X→Y的紧运算元；

4)设X、Y、Z为赋范线性空间，T₁∈L(X，Y)，T₂∈L(Y，Z)，如果T₁，T₂中至少有一个为紧运算元，则T₂T₁为X→Z的紧运算元。

5)设X为赋范线性空间，Y为巴拿赫空间，而且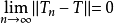，则T也是紧运算元；

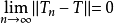
6)设T∈L(X，Y)，T为紧运算元，则T的值域是可分的；

7)设T∈L(X，Y)，T为紧运算元，则T*为Y*→X*的紧运算元；

8)设T∈L(X，Y)，如果T为紧运算元，则T将X中的弱收敛点列映成Y中的强收敛点列；

9)设X为赋范线性空间，Y为巴拿赫空间，则X→Y的紧运算元的全体按通常运算元的线性运算按运算元範数构成了L(X，Y)的闭子空间，因此它本身也是一个巴拿赫空间。

全连续性是线性积分运算元特有的基本性质。设k(x，y)是G×G上的平方可积函式，则以k(x，y)为核的线性积分运算元是映L²(G)入L²(G)的全连续线性运算元。类似地，若k(x，y)在G×G上连续，则以k(x，y)为核的线性积分运算元是映C(G)入C(G)的全连续运算元.线性积分运算元所具有的全连续性，使得线性积分运算元可以作为全连续线性运算元的一种特例而加以研究。人们可以首先用泛函分析的方法研究全连续线性运算元，然后作为套用的特例，导出线性积分运算元的基本性质。