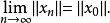点列(range of points)是射影几何的基本概念之一,指一条直线上所有点的集合。该直线称为点列的底。收敛点列一定是基本点列,但基本点列不一定有极限。由点列强收敛可推出其弱收敛。
基本介绍
- 中文名:点列
- 外文名:range of points)
- 概述:一条直线上所有点的集合
- 符号表示:l(A,B,C,...)
- 领域:射影几何
- 学科:数学
定义
点列(range of points)是射影几何的基本概念之一,指一条直线上所有点的集合。该直线称为点列的底,以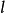 为底,以点A,B,C,…为元素的点列记为
为底,以点A,B,C,…为元素的点列记为
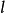
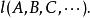
基本点列
设(x,ρ)是距离空间,{xn}是X中的点列,如果对任意正数ε,存在自然数N,使得m,n≥N时,
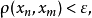
注:收敛点列一定是基本点列,但基本点列不一定有极限。
点列的收敛性
弱收敛:设X为赋范线性空间,xn,x∈X,若对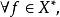 有
有
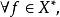
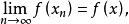
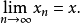
强收敛:设X为赋范线性空间,xn,x∈X,当
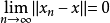
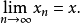
注:1.由点列强收敛可推出其弱收敛。[1]
证明:由
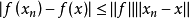
2.设X为赋范线性空间,xn,x∈X,则w-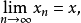 若且唯若
若且唯若
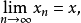
(1)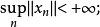
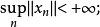
(2)存在X*上一个稠密集Y,使得
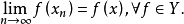
3.设X为一致凸的赋范线性空间,则X中的点列{xn}强收敛于x0的充要条件是{xn}弱收敛于x0,且有