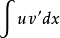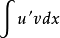不定积分的运算法则,别称不定积分的性质,f(x)的原函式,存在微分的反函式。
基本介绍
- 中文名:不定积分的运算法则
- 别称:不定积分的性质
- 性质:f(x)的原函式,存在微分的反函式
- 适用条件:分开k≠0或k=0
不定积分的运算法则,包含如下两个性质(注意性质适用条件):
1、设函式f(x)的原函式存在(即f(x)可积,下同),k是常数,则:
(1)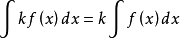 (k≠0)
(k≠0)
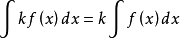
(2)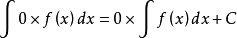 (k=0)
(k=0)
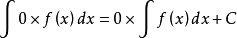
2、设f(x),g(x)两个函式存在原函式,则:
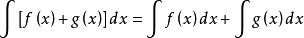
3、常见积分几种运算法
换元积分法:
①设f(u)具有原函式F(u) ,如果u是中间变数:u=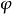 (x),且
(x),且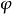 (x)可微,那幺,根据複合函式微分法,有
(x)可微,那幺,根据複合函式微分法,有
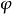
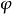
dF=[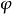 (x)]=f[
(x)]=f[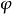 (x)]
(x)]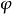 '(x)dx,从而根据不定积分的定义就得:
'(x)dx,从而根据不定积分的定义就得:
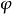
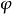
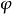
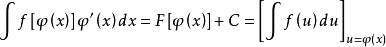
若要求
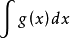

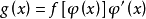
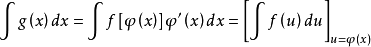
这种方法称为第一类换元法。
②利用第二类换元法化简不定积分的关键仍然是选择适当的变换公式 x = φ(t)。此方法主要是求无理函式(带有根号的函式)的不定积分。由于含有根式的积分比较困难,因此我们设法作代换消去根式,使之变成容易计算的积分。 下面简单介绍第二类换元法中常用的方法:
(1)根式代换:被积函式中带有根式 ,可直接令 t =
,可直接令 t =


(2)三角代换:利用三角函式代换,变根式积分为有理函式积分,有三种类型: 被积函式含根式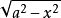 ,令
,令 ;被积函式含根式
;被积函式含根式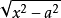 ,令
,令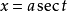 。
。
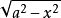

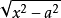
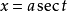
注:记住三角形示意图可为变数还原提供方便。
(3)倒代换(即令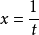 ):设m,n 分别为被积函式的分子、分母关于x 的最高次数,当 n-m>1时,用倒代换可望成功
):设m,n 分别为被积函式的分子、分母关于x 的最高次数,当 n-m>1时,用倒代换可望成功
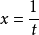
(4)指数代换:适用于被积函式由指数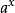 所构成的代数式;
所构成的代数式;
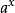
(5)万能代换(半角代换):被积函式是三角函式有理式,可令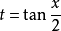 ,则:
,则:
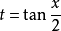
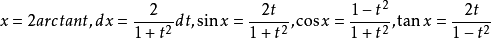
分部积分法:
设函式u=u(x)及v=v(x)具有连续导数,则其乘积的导数为:
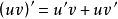
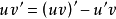
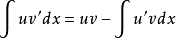
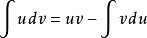
如果求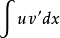 有困难,而求
有困难,而求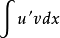 比较容易时,分部积分公式就可以发挥作用了。
比较容易时,分部积分公式就可以发挥作用了。