进行二元多段翼增升装置试验的设备是多样的。但考虑到利用现有三元风洞进行二元试验的试验装置有见效快、经济性好等优点，NH-2风洞採用了在上、下洞壁间安装两块辅助壁板，形成所谓嵌入式二元试验段装置，这是英美风洞中习惯採用的一种方法。如图。

这种试验装置的宽高比主要考虑洞壁干扰的影响：

（1）由于上、下洞壁的存在，不仅引起流向的变化，而且会引起流线曲率的改变。在大迎角和大襟翼偏角时，影响尤为严重。从这一点考虑，模型弦长b与试验段高度H之比不应大于0. 3。在大襟翼偏角时，比值控制在0. 25以内较为合适;另外，上、下洞壁的附面层会因模型的存在而产生分离，多段冀的试验升力係数较大，分离更为严重。从这一点考虑，为使附面层不分离，应小于2为宜。

（2）由于两侧壁板的存在，模型与侧壁连线处的附面层发生分离。从作者所做的流谱观察来看，两侧壁的影响很明显，使模型的二元区大为减小，从这一点考虑，模型的展弦比应取得大一些为好，一般应大于2。

试验装置的宽高比及模型的展弦比要综合考虑上述要求进行设计。

二元嵌入板在顺气流方向上的长度将影响二元试验结果。研究表明,模型之后的侧壁长度对试验结果影响不明显，而模型之前的侧壁长度却有明显的影响。如图所示,如果前侧壁长度小于2b，升力係数将急剧下降，而且随档板逐渐缩短，升力係数下降的迎角提前。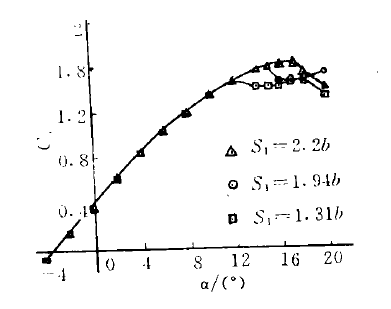

模型前侧壁长度影响

二元侧壁厚度从减小堵塞，提高流场品质考虑越薄越好，但要有足够的刚性，否则会导致侧壁的变形和振动。侧壁前缘形状无论是圆形还是尖劈形，对二元流场影响不大。

NH-2风洞二元试验装置设计成两侧可调，前后长度也可调，头部形状可换，它可适应和满足各种模型试验的要求。

NACA0012翼型是在国内外被广泛地用作二元翼型理论计算和风洞试验研究比较的典型翼型之一，但发表的变开闭比风洞试验结果为数极少。近年来，AEDC等单位所作的变开闭比超临界翼型试验结果表明，洞壁干扰对模型气动力性能的影响与雷诺数的影响相当，甚至更大。

为探讨跨音速洞壁干扰效应，1981年7月在南航NH一1风洞进行了NACA0012翼型试验，以估计模型尺寸和洞壁开闭比对风洞试验数据的影响。当风洞来流马赫数M<1.0时，模型表面上的局部冲波不会从洞壁上反射，即不存在洞壁反射波干扰。在这种状态下的洞壁干扰主要是模型的堵塞干扰和升力约束干扰。堵塞干扰效应是在攻角等于0度时，用三个几何相似而堵塞度不同的模型,在不同开闭比下进行实验研究。而升力约束干扰效应是在有攻角情况下取得的。

荣柏森在南京航空学院NH一1三音速风洞进行了NACA0012冀型跨音速风洞实验，讨论了洞壁开闭比和模型尺寸对驻室参考点静压、翼型表面压力分布的影响。结果表明，开闭比和模型尺寸对驻室静压有明显影响，开闭比对翼型表面压力分布有很大影响。在攻角零度时，超临界流动条件下，当开闭比从6%变到0.5%时，翼型上表面激波位置向后移动範围达20%的弦长；开闭比为4%时，翼型接近于无堵塞干扰。当攻角1度和马赫数为0.759时，消除洞壁干扰的最佳开闭比为4%。因此，开闭比改变引起的洞壁效应对翼型气动力特性的影响是值得重视的。

风洞试验是确定飞行器气动参数的重要途径，然而，风洞试验数据因为各种原因存在一定的不确定性，人们围绕提高风洞试验数据的精度和準度进行了不懈的努力。为了更客观地使用风洞试验数据，国外首先引入了不确定性分析方法。在不确定性分析过程中，最重要的技术环节就是获得相应的敏感性导数，对于导数的求取方法，最直接的方式就是利用差分法获取，随着计算流体力学(Computational Fluid Dynamics,CFD)技术的发展和成熟，利用CFD工具计算这些敏感性导数，理论上是可以实现的，但是，对于众多的敏感性导数，如果採用简单的差分算法意味着巨大的计算量以及过于繁杂的人工操作。此外，CFD软体计算的结果还受到格线数量、收敛精度等因素的影响，而且差分算法中步长的选取也对敏感性导数值产生影响。为了更有效地获得敏感性导数，国外引入自动微分方法，这种方法直接伴随CFD求解空气动力学基本方程的实际过程，敏感性导数的计算也是数学意义上严格的微分概念，更有意义的是，只要开发出的计算程式设计合适，可以在一次性计算中同时获得大量的敏感性导数，而且敏感性导数的收敛精度与流场的收敛精度达到相同的量级，因此，敏感性导数的计算精度可以得到充分保证。同时，相对于同样具有高精度，但计算量过大的复步长微分方法和难以推广到複杂问题的符号微分方法，自动微分对具体问题的适应性和可行性最好。国内对自动微分的研究套用始于21世纪初，在气动最佳化领域己取得一些进展，对风洞试验不确定性分析的研究和成果主要围绕试验误差分析和不确定度合成方法，并且主要套用在积分型气动力係数不确定度的计算上。

为了深入分析风洞试验中来流参数的扰动对翼型气动试验结果的影响，基于雷诺平均Navier－Stokes方程有限体积方法，採用Spalart－Allmaras湍流模型，发展了一套二维计算流体力学（CFD）程式，套用自动微分方法对CFD程式进行改造，建立了对应过程的敏感性导数计算方法和程式，可以一次性获得翼型各处压力係数和所有气动力係数对迎角、马赫数和雷诺数的敏感性导数。研究结果表明：在亚声速和跨声速中，翼型压力分布对马赫数最敏感，比对雷诺数的敏感性至少高8个量级，但是，在亚声速来流中，翼型压力係数的不确定性由迎角摄动引起的部分比马赫数摄动引起的部分高1个量级，迎角控制精度很大程度上决定了风洞试验结果的精度；在跨声速来流中，迎角摄动引起的不确定性比马赫数摄动引起的要低1个量级，同时，对马赫数敏感性的增强使得翼型压力分布的不确定性在跨声速範围比在亚声速範围高1个量级，此时马赫数的控制精度很大程度上决定了风洞试验结果的精度。