T1定理(T1 theorem)是判别一类非卷积型积分运算元L2有界的定理,由达维德和儒尔内得到。
基本介绍
- 中文名:T1定理
- 外文名:T1 theorem
- 适用範围:数理科学
简介
概况
T1定理是判别一类非卷积型积分运算元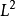 有界的定理,由达维德和儒尔内得到。
有界的定理,由达维德和儒尔内得到。
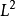
具体内容
T1定理叙述如下:
设T为𝒟→𝒟'的连续线性运算元,如果存在考尔德伦-赞格蒙核K(x,y),满足:对

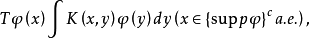

1、

2、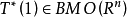
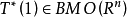
3、T为弱有界,其中 T* 为T 的共轭运算元,T 为弱有界是指对𝒟中的任一有界集 F,存在常数C,使得
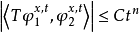
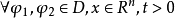
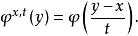
运算元
广义的讲,对任何函式进行某一项操作都可以认为是一个运算元,甚至包括求幂次,开方都可以认为是一个运算元,只是有的运算元用了一个符号来代替他所要进行的运算,所以运算元和f(x)的f没区别,它甚至和加减乘除的基本运算符号都没有区别,只是他可以对单对象操作(有的符号比如大于、小于号要对多对象操作)。
又比如取机率P{X<x},机率是集合{X<x}(他是属于实数集的子集)对[0,1]区间的一个映射,实数域和[0,1]区间是可以一一映射的,所以取机率符号P认为也是一个运算元,和微分,积分运算元运算元没区别。总而言之,运算元就是映射,就是关係,就是变换。
