自洽场方法(self-consistent field method, SCF),即自洽场近似法,是量子力学中叠代求解多粒子系统薛丁格方程的基本方法。其基本思想是首先按照某种方法给出波函式的一个估计,然后利用这个估计来计算电子密度,再通过电子密度来得到哈密顿量中与粒子间相互作用有关的项,再进行薛丁格方程的求解得到一组改进的估计。很多情况下,自洽场方法一词也用于直接指代哈特里-福克方法。
基本介绍
- 中文名:量子力学的自洽场近似法
- 外文名:self-consistent field method
- 领域:量子力学
- 别称:自洽场方法
- 用于:求解全同多粒子系
例子
在哈特里-福克方法中,上述步骤具体表现为:
- 给出波函式的估计 → 给出分子轨道中基函式线性组合係数的一个估计;
- 用估计来计算电子密度 → 计算密度矩阵;
- 计算相互作用项 → 计算福克矩阵元;
- 得到改进的估计 → 对角化福克矩阵得到其本徵矢,作为新的基函式线性组合係数的估计。
种类
- 哈特里自洽场方法 (哈特里-福克方法的前身)
- 哈特里-福克方法
- 多组态自洽场方法
简介
哈特里-福克方程(英语:Hartree–Fock equation),又称为HF方程,是一个套用变分法计算多电子系统波函式的方程,是量子物理、凝聚态物理学、量子化学中最重要的方程之一。HF方程形式上是单电子本徵方程,求得的本徵态是单电子波函式,即分子轨道。以HF方程为核心的数值计算方法称为“哈特里-福克方法”(Hartree–Fock method)。
基于分子轨道理论的所有量子化学计算方法都是以HF方法为基础的。鑒于分子轨道理论在现代量子化学中的广泛套用,HF方程被视为现代量子化学的基石。
哈特里-福克近似
哈特里-福克近似也称为分子轨道近似或单行列式近似,认为多电子体系波函式可以由体系分子轨道波函式构造的单个斯莱特行列式表示:
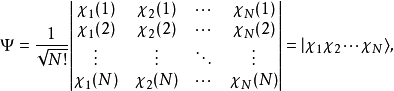
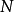

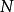
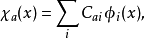
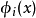
在此近似下,由变分法,体系的多电子薛丁格方程可化为单电子方程:
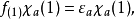
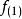
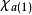
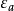
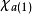
方程的套用
HF方程在量子化学中有着广泛的套用,所有分子轨道理论的量子化学计算都是以HF方程为基础的。
- 组态相互作用方法(CI):在CI方法中,通过HF方程解得的一系列分子轨道用于构建多电子基函式集,在构建了多电子基函式集后再通过变分法处理获得CI能量的最低点,因而进行CI计算必须首先完成HF方程的求解。
- 多体微扰理论方法(MPn):MPn计算将体系所有福克算符的代数和定义为哈特里-福克哈密顿算符,将电子间相互作用所产生的能量项看作是对哈特里-福克哈密顿算符的微扰,经过微扰处理后可以获得体系能量的近似值。进行多体微扰计算也需要首先进行HF方程的求解,以获得需要的分子轨道波函式形式和分子轨道能量。
- 半经验量子化学计算:半经验量子化学计算是对HF方程求解过程的简化。在HF方程的求解中,绝大部分计算量都分布在由正则HF方程向矩阵本徵方程形式转变的过程中,如果将这一过程中大量的电子积分用经验数值代替,便可以极大地缩短HF方法的计算时间。为此,针对不同的研究体系,量子化学家开发了不同的积分经验常数,与之相应地产生了各种半经验量子化学计算方法。本质上讲,半经验计算仍然是通过自洽场方法求解HF方程的过程。
多组态自洽场
多组态自洽场方法(Multi-configurational self-consistent field,MCSCF)是量子化学中的一种计算方法,主要用于在哈特里-福克方法和密度泛函理论不足以给出良好的参考态函式的时候(例如,在键断裂过程中,或者分子基态与低激发态能量近简併的情形)产生定量正确的参考态函式。它用一组组态态函式的线性组合来近似真实的电子波函式。在 MCSCF 方法中,既改变组态态函式前的线性组合係数,也改变每一个组态态函数里面的基函式前的线性组合係数,同时改变两者以使能量达到最小值,就得到变分的电子波函式。这个方法可以视作组态相互作用方法和哈特里-福克方法的组合。
MCSCF 波函式经常用作多参考组态相互作用或多参考态微扰理论(如完全活性空间微扰理论)计算的参考态,这些方法可以处理一些很极端的情形,并且,抛开计算资源的限制不谈,这些方法能够在其它方法失效的情况下得到可靠的分子基态与激发态波函式。
完全活性空间
一种特别重要的 MCSCF 方法是完全活性空间自洽场方法(CASSCF)。完全活性空间又称为全最佳化反应空间(full-optimized reaction space),相应的方法称为FORS-MCSCF。CASSCF 与 FORS-MCSCF是同义词。在 CASSCF 方法中,展开式中包括所有给定数目的电子在给定数目的轨道上分布所得的所有组态态函式。例如,对一氧化氮分子进行 CASSCF(11,8) 计算意味着波函式展开式中包含11个价电子在8个分子轨道上自由分配所能得到的全部状态态函式。
