斜下三角行列式和斜上三角行列式的数值一样，
为(-1)^(n(n-1))/2 a1n a2,n-1...an-1,2 an1
基本介绍
- 外文名：Oblique triangular determinant
- 别称：次下三角行列式
- 套用学科：线性代数
- 适用领域範围：行列式
定律定义
对于n阶的斜下三角行列式下列公式。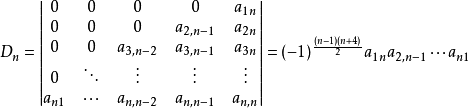
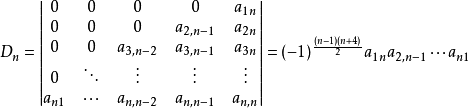
特别地，斜对角行列式
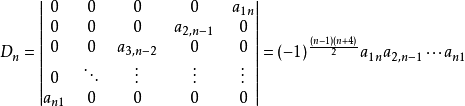
推导过程
降阶法
按定义将第一行反覆展开。
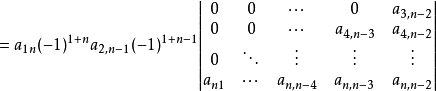
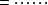
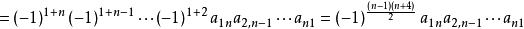
由于乘上（-1）-2n+2=1不改变上式的符号，亦可写作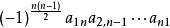
。
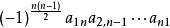
数学归纳法
猜想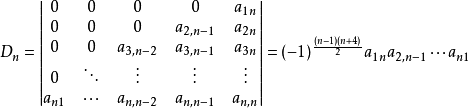： 成立。当n=1时，D1=|a1n|=(-1)0a1n=a1n,成立。
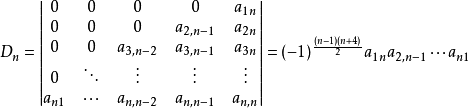
假设n=k-1（k
且k>1）等式也成立。由假设,少一阶的行列式：
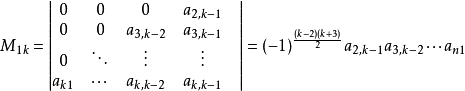
当n=k时，按行列式定义展开第一行，Dk=（-1）a1kM1K。
从而，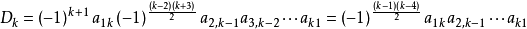
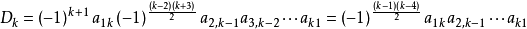
有数学归纳法得，猜想成立，证毕。