行列式在数学中，是由解线性方程组产生的一种算式。行列式的特性可以被概括为一个多次交替线性形式，这个本质使得行列式在欧几里德空间中可以成为描述“体积”的函式。
其定义域为nxn的矩阵A，取值为一个标量，写作det(A)或 | A | 。行列式可以看作是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说，在n维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响。无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的套用。 行列式概念最早出现在解线性方程组的过程中。十七世纪晚期，关孝和与莱布尼茨的着作中已经使用行列式来确定线性方程组解的个数以及形式。十八世纪开始，行列式开始作为独立的数学概念被研究。
十九世纪以后，行列式理论进一步得到发展和完善。矩阵概念的引入使得更多有关行列式的性质被发现，行列式在许多领域都逐渐显现出重要的意义和作用，出现了线性自同态和向量组的行列式的定义[1] 。
续文
因中文百科词条公式数量限制，行列式词条内容剩余部分展示在此词条中。
基本性质
行列式的一些基本性质，可以由它的多线性以及交替性推出。
- 在行列式中，一行（列）元素全为0，则此行列式的值为0。
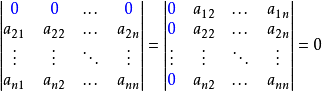
- 在行列式中，某一行（列）有公因子k，则可以提出k。
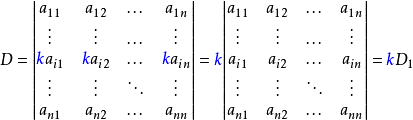
- 在行列式中，某一行（列）的每个元素是两数之和，则此行列式可拆分为两个相加的行列式。
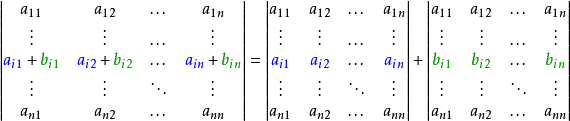
- 行列式中的两行（列）互换，改变行列式正负符号。
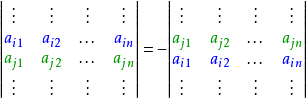
- 在行列式中，有两行（列）对应成比例或相同，则此行列式的值为0。
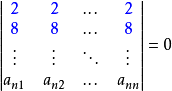
- 将一行（列）的k倍加进另一行（列）里，行列式的值不变。
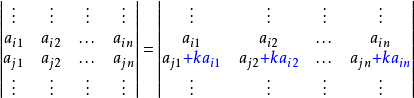
- 注意：一行（列）的k倍加上另一行（列），行列式的值改变。
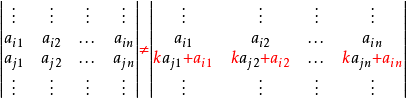
- 将行列式的行列互换，行列式的值不变，其中行列互换相当于转置。这个性质可以简单地记作
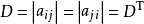
- 行列式的乘法定理：方块矩阵的乘积的行列式等于行列式的乘积。
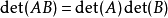
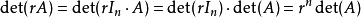
·以上的乘法公式还可以进一步推广为所谓柯西–比内公式，从而使得只要两个矩阵的乘积是方块矩阵，就有类似于以上的结果：假设A是一个矩阵，而B是一个矩阵。如果S是
中具有m个元素的子集
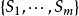，我们记AS为A中列指标位于S中的子矩阵。类似地，记BS为B中行指标位于S中的子矩阵。那幺
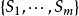
这里求遍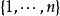
中m个元素的所有可能子集S（共有C(n,m)个）。
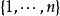
如果m=n，即A与B是同样大小的方块矩阵，则只有一个容许集合S，柯西–比内公式退化为通常行列式的乘法公式。如过m= 1则有n容许集合S，这个公式退化为点积。如果m>n，没有容许集合S，约定行列式det(AB)是零。
·若A是可逆矩阵，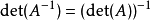
。
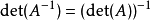
·由行列式的乘法定理以及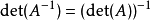
可以知道，行列式定义了一个从一般线性群
到上
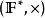的群同态。
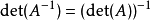
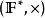
·若将方块矩阵中的元素取共轭，得到的是矩阵的共轭矩阵。共轭矩阵的行列式值等于矩阵行列式值的共轭：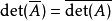
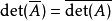
·若两个矩阵相似，那幺它们的行列式相同。这是因为两个相似的矩阵之间只相差一个基底变换，而行列式描述的是矩阵对应的线性映射对体积的影响，而不是体积，所以基底变换并不会影响行列式的值。用数学语言来说，就是：
如果两个矩阵A与B相似，那幺存在可逆矩阵P使得，所以
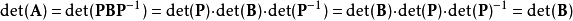
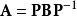
·行列式是所有特徵值（按代数重数计）的乘积。这可由矩阵必和其若尔当标準型相似推导出。特殊地，三角矩阵的行列式等于其对角线上所有元素的乘积。
·由于三角矩阵的行列式计算简便，当矩阵的係数为域时，可以通过高斯消去法将矩阵变换成三角矩阵，或者将矩阵分解成三角矩阵的乘积之后再利用行列式的乘法定理进行计算。可以证明，所有的矩阵A都可以分解成一个上三角矩阵U、一个下三角矩阵L以及一个置换矩阵P的乘积：
。这时，矩阵A的行列式可以写成：
·分块矩阵的行列式并不能简单地表示成每个分块的行列式的乘积组合。对于分块的三角矩阵，仍然有类似的结论：
，矩阵的行列式等于对角元素的行列式之乘积。
对于一般情况，若对角元素中有一个是可逆矩阵，比如说A可逆，那幺矩阵的行列式可以写做
·矩阵的行列式和矩阵的迹数有一定的关联，当矩阵的係数为域时，在定义了矩阵的指数函式后，有如下的恆等式：
行列式的展开
余因式
又称“余子式”、“余因子”。参见主条目余因式。
对一个n阶的行列式M，去掉M的第i行第j列后形成的n-1阶的行列式叫做M关于元素mij的余因式。记作
。
代数余子式
M关于元素mij的代数余子式记作
。
行列式关于行和列的展开
一个n阶的行列式M可以写成一行（或一列）的元素与对应的代数余子式的乘积之和，叫作行列式按一行（或一列）的展开。
这个公式又称拉普拉斯公式，把n维矩阵的行列式计算变为了n个n-1维的行列式的计算。另一方面，拉普拉斯公式可以作为行列式的一种归纳定义：在定义了二维行列式后，n维矩阵的行列式可以藉助拉普拉斯公式用n-1维的行列式来定义。这样定义的行列式与前面的定义是等价的。
计算
计算行列式的值是一个常见的问题。最简单的方法是按照定义
计算或按照拉普拉斯公式进行递归运算。这样的算法需要计算
次的加法，複杂度是指数函式。在实际的计算中只能用于计算阶数很小的行列式。注意到拉普拉斯公式的性质，如果一行或一列里面有很多个0，那幺就可以把行列式按这一行或一列展开，这时数值为零的係数所对应的代数余子式就不必计算了，因为最后要乘以0，这样就可以简化计算。然而更加简便的算法是利用高斯消去法或LU分解法，把矩阵通过初等变换变成三角矩阵或三角矩阵的乘积来计算行列式的值。这些算法的複杂度都是n3级别，远远小于直接计算的複杂度。
如果一个算法可以在
时间内算出矩阵乘法，那幺可以构造出一种
时间内的行列式求值算法。这说明求矩阵的行列式的值和矩阵的乘法有相同的複杂度。于是，通过分治算法或者其它的方法，可以达到比
更好的结果。比如，存在複杂度
的行列式求值算法。
函式
由行列式的一般表达形式中可以看出，矩阵A的行列式是关于其元素的多项式。因此行列式函式具有良好的光滑性质。
单变数的行列式函式
设矩阵函式
为
（k阶连续可导）的函式，则由于行列式函式
只不过是矩阵
的某些係数的乘积，所以也是
的。其对t的导数为
，其中的每个
是矩阵
的第i个行向量（也可以全部是列向量）。
矩阵的行列式函式
函式
是连续的。由此，n阶一般线性群是一个开集，因为是开区间
的原像，而特殊线性群则是一个闭集，因为是闭集合
的原像。
函式
也是可微的，甚至是光滑的（
）。它在某个矩阵A处的展开为
也就是说，在装备正则範数的矩阵空间Mn()中，伴随矩阵是行列式函式的梯度
可逆矩阵的可微性说明一般线性群GLn()是一个李群。