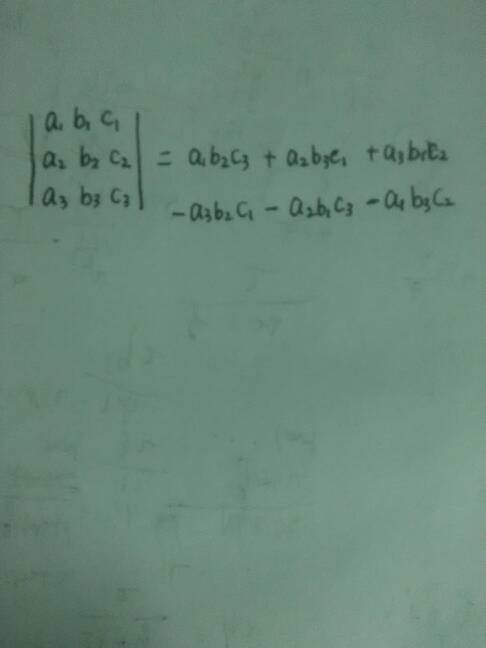如右图利用加减消元法,为了容易记住其求解公式,但要记住这个求解公式是很困难的,因此引入三阶行列式的概念。
记称左式的左边为三阶行列式,右边的式子为三阶行列式的展开式。
基本介绍
- 中文名:三阶行列式
- 外文名:Three order determinant
- 套用学科:数学
- 适用领域範围:线性代数、高等数学
- 计算方法数目:两种
- 套用区域:矩阵相乘、求三角形面积
计算方法
直接计算——对角线法
标準方法是在已给行列式的右边添加已给行列式的第一列、第二列。我们把行列式的左上角到右下角的对角线称为主对角线,把右上角到左下角的对角线称为次对角线。这时,三阶行列式的值等于主对角线的三个数的积与和主对角线平行的对角线上的三个数的积的和减去次对角线的三个数的积与和次对角线平行的对角线上三个数的积的和的差。
 三元方程组
三元方程组任何一行或一列展开——代数余子式
行列式某元素的余子式:行列式划去该元素所在的行与列的各元素,剩下的元素按原样排列,得到的新行列式.
行列式某元素的代数余子式:行列式某元素的余子式与该元素对应的正负符号的乘积.
行列式某元素的代数余子式:行列式某元素的余子式与该元素对应的正负符号的乘积.
即行列式可以按某一行或某一列展开成元素与其对应的代数余子式的乘积之和。 三阶行列式运算
三阶行列式运算
 三阶行列式运算
三阶行列式运算举例

结果为 a1·b2·c3+b1·c2·a3+c1·a2·b3-a3·b2·c1-b3·c2·a1-c3·a2·b1(注意对角线就容易记住了)
这里一共是六项相加减,整理下可以这幺记:
a1(b2·c3-b3·c2) - a2(b1·c3-b3·c1) + a3(b1·c2-b2·c1)=
a1(b2·c3-b3·c2) - b1(a2·c3 - a3·c2) + c1(a2·b3 - a3·b2)
此时可以记住为:
a1*(a1的余子式)-a2*(a2的余子式)+a3*(a3的余子式)=
a1*(a1的余子式)-b1*(b1的余子式)+c1*(c1的余子式)
某个数的余子式是指删去那个数所在的行和列后剩下的行列式。
行列式的每一项要求:不同行不同列的数字相乘
如选了a1则与其相乘的数只能在2,3行2,3列中找,(即在 b2 b3 c2c3中找)
而a1(b2·c3-b3·c2) - a2(b1c3-b3·c1) + a3(b1·c2-b2·c1)是用了行列式展开运算:即行列式等于它第一行的每一个数乘以它的余子式,或等于第一列的每一个数乘以它的余子式,然后按照 + - + - + -......的规律给每一项添加符号之后再做求和计算。
性质
性质1 行列式与它的转置行列式相等。
性质2 互换行列式的两行(列),行列式变号。
推论 如果行列式有两行(列)完全相同,则此行列式为零。
性质3 行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘此行列式。
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。
性质4 行列式中如果有两行(列)元素成比例,则此行列式等于零。
性质5 把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变。
套用
求三角形面积
三阶行列式:三阶行列式的展开式也可用对角线法则得到,三阶行列式的对角线法则如下图所示:
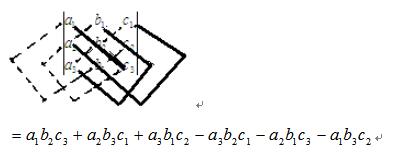 三阶行列式的对角线法则
三阶行列式的对角线法则三角形的面积求法
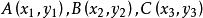

求两个矩阵相乘
方法1:
把两个行列式,都分别求出来,然后相乘
方法2:
矩阵A乘矩阵B,得矩阵C,方法是A的第一行元素分别对应乘以B的第一列元素各元素,相加得C11,A的第一行元素对应乘以B的第二行各元素,相加得C12,以此类推,C的第二行元素为A的第二行元素按上面方法与B相乘所得结果,以此类推.N阶矩阵都是这样乘,A的列数要与B的行数相等.