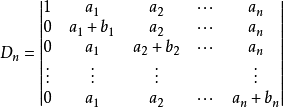计算行列式通常用降阶法，但有时也可反其道而行之，将它的阶数放大，增加一行一列，使升阶后的行列式与原行列式相等，且易于计算(即适当选择所增加的行列元素，使下一步化简后出现大量的零元素)，这种方法叫做升阶法或加边法。它的理论依据是行列式依行(列)展开定理。通常在行列式各行(列)中相同元素较多时，可考虑利用加边法。
基本介绍
- 中文名：升阶法
- 所属学科：数学
- 别名：加边法
- 相关问题：计算行列式
基本介绍
行列式计算的一般方法是降阶，但对于某些特殊的n阶行列武，如除对角元素(或次对角元素)外，其余元素相同或成比例的行列式。有时加上一行一列变成
阶的行列式，特别是第1列为
并适当选择第1行的元素，就可以使消零化筒更方便，且化简后常变成箭形行列式。这一方法称为升阶法或加边法。
例题解析
【例1】计算n阶行列式
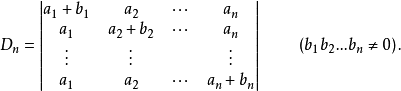
分析： 该行列式除对角元之处。各行的元素均为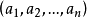
。
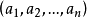
【解】（先升阶）
