斯莱特行列式是多电子体系波函式的一种表达方式,他以量子物理学家斯莱特的名字命名。这种形式的波函式可以满足对多电子波函式的反对称要求(即所谓泡利原理):交换体系中任意两个电子的坐标,则波函式的符号将会反转。在量子化学中,所有基于分子轨道理论的计算方法都用斯莱特行列式的形式来表示多电子体系的波函式。
基本介绍
- 中文名:斯莱特行列式
- 外文名:slater determinant
- 定义:多电子体系波函式的一种表达方式
- 作用:满足对多电子波函式的反对称要求
- 表示对象:分子轨道理论的计算方法
- 套用学科:数学
形式
基本形式
斯莱特行列式最原初的形态是一个由单电子波函式即分子轨道波函式构成的行列式:
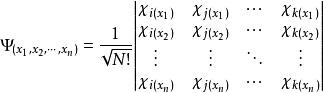
行列式中每一行是由同一电子的不同可能波函式组成,每一列是由不同电子的相同可能波函式组成,行列式前的係数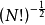 是保证波函式归一性的归一係数。
是保证波函式归一性的归一係数。
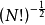
根据行列式的性质,互换行列式中的两行行列式的符号会反转:
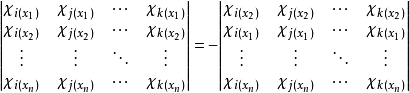
这一性质正符合多电子体系的泡利原理。
其他形式
考虑到行列式在书写过程中的不便,通常人们用右矢的形式代表斯莱特行列式:

需要注意的是,这种右矢形式仅仅用来代表行列式,并非数学上的相等关係。
将行列式展开后,可以用置换运算元形式来表示斯莱特行列式:

其中运算元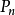 叫做置换运算元,其作用是将各分子轨道波函式中的电子序号进行交换,根据排列的原理,在由N个电子组成的体系中,这样的运算元一共有N!个。
叫做置换运算元,其作用是将各分子轨道波函式中的电子序号进行交换,根据排列的原理,在由N个电子组成的体系中,这样的运算元一共有N!个。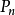 是置换运算元的奇偶性,即任何置换运算元可以转化为若干两两对换的置换运算元的乘积,所谓奇偶性就是一个置换运算元所分解成的对换运算元的个数的奇偶性。与上面提到的右矢形式不同,这种由置换运算元来表达的形式与行列式表达式在数学上是严格相等的。
是置换运算元的奇偶性,即任何置换运算元可以转化为若干两两对换的置换运算元的乘积,所谓奇偶性就是一个置换运算元所分解成的对换运算元的个数的奇偶性。与上面提到的右矢形式不同,这种由置换运算元来表达的形式与行列式表达式在数学上是严格相等的。
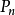
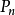
对Slater行列式的置换运算元形式进一步简化可以用反对称化运算元形式来表示:
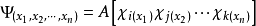
其中运算元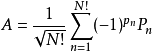 叫做反对称化运算元。
叫做反对称化运算元。
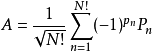
套用
斯莱特行列式在量子化学中套用广泛,经过自洽场方法解HF方程获得的最终解便是一个斯莱特行列式型多电子波函式,高级的量子化学计算方法也套用到斯莱特行列式,组态相互作用方法得到的多电子体系波函式是若干个斯莱特行列式的线性组合:
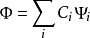
经过对这个由许多行列式组成的巨大波函式的变分法处理,可以获得比HF方程更加精确的量子化学计算结果

