行列式依行展开(expansion of a determinant by a row)是计算行列式的一种方法,设ai1,ai2,…,ain (1≤i≤n)为n阶行列式D=|aij|的任意一行中的元素,而Ai1,Ai2,…,Ain分别为它们在D中的代数余子式,则D=ai1Ai1+ai2Ai2+…+ainAin称为行列式D的依行展开。如果行列式D的第i行各元素与第j行各元素的代数余子式对应相乘后再相加,则当i≠j时,其和为零,行列式依行或依列展开不仅对行列式计算有重要作用,且在行列式理论中也有重要的套用。
基本介绍
- 中文名:行列式依行展开
- 外文名:expansion of a determinant by a row
- 所属学科:数学
- 所属问题:高等代数(行列式)
- 简介:计算行列式的一种方法
基本介绍
设ai1,ai2,…,ain(1≤i≤n)为n阶行列式D=|aij|的任意一行中的元素,而Ai1,Ai2,…,Ain分别为它们在D中的代数余子式,则D=ai1Ai1+ai2Ai2+…+ainAin称为行列式D的依行展开。
例如,在一个三阶行列式D中,划去元素aij(i=1, 2,3; j=1, 2,3)所在的第i行和第j列的所有元素,剩下的元素按照它原有的位置得到的一个二阶行列式称为元素aij的余子式,记作Mij。而将(-1)i+jMij称为元素aij的代数余子式,记作Aij,即Aij=(-1)i+jMij。例如

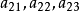
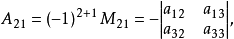
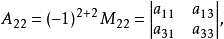
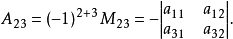
D= ai1Ai1+ ai2Ai2 + ai3Ai3 ( i=1,2,3 ), (1)
D= a1jA1j+ a2jA2j + a3jA3j( j=1,2,3 ), (1')
我们把类似(1)式的展开称为行列式的依行展开式,把(1')式称为行列式的依列展开式。
相关定理
定理1(行列式依行展开定理) n(n>1)阶行列式D=|aij|等于它任意一行的所有元素与它们对应的代数余子式的乘积的和,即
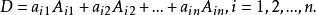
定理2如果行列式D的第i行各元素与第j行各元素的代数余子式对应相乘后再相加,则当i≠j时,其和为零。因此有
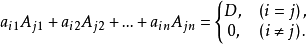
【例1】 设
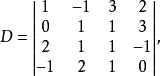
依第二行展开,并求D的值。
解: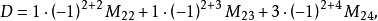
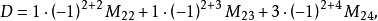
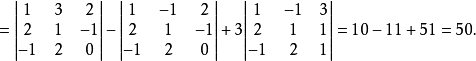
说明 直接利用行列式依行展开公式计算并不简便,因此,在实行计算中,经常是先利用性质化简,再依行展开,即把某一行通过变换,化出较多的0来,再降阶计算。

