Klein隧穿，即在相对论物体可以通过所有势垒，不管势垒有多高或多宽：而在非相对论量子隧道理论中，低能粒子穿透高能势垒的几率永远不会是100%，随着势垒变高变厚，穿越的可能性也随之减小。但Klein隧穿中认为相对论粒子可以很轻易地穿越又高又宽的势垒，成功率高达100%。粒子遇到势垒时，就会转换成它的反粒子，真实世界里的山峰，在反粒子看来就成了山谷。反粒子很容易就通过这个反物质世界的“山谷”，到达势垒的另外一边后，再变回普通粒子，看上去就跟没有遇到障碍似的。即使在许多物理学家看来，量子电动力学里的这些预言看上去也是极度不合常理的。 现在，石墨烯中无质量狄拉克準粒子终于证实了这一预言。在石墨烯中，Klein隧穿所描述的现象很容易被观察到。 所有粒子都发生了量子隧道效应，通过率达100%。现在，研究人员正在测量粒子通过不同高度的势垒时产生的电流。物理学家还希望，石墨烯能够帮助他们证明量子电动力学所预言的其他一些奇特现象。
基本介绍
- 中文名：Klein 隧穿
- 外文名：Klein Tunneling
- 别名：克莱因隧穿，克莱因佯谬
- 提出人：OskarKlein
- 提出时间：1929
定义
1929年，物理学家Oskar Klein在研究势垒中的电子散射这一常规问题时，他将狄拉克方程套用其中，获得了一个非常令人惊讶的结果。在非相对论量子力学当中，在势垒中电子隧穿是呈指数衰减的。然而，Klein所获得的结果却是，电势与电子质量是相当的，即
，也就是说电势可以认为是透明的。此外，当势垒呈无穷大时，虽然反射减小了，但是电子确是始终在传输的。这就是klein隧穿，也被称之为Klein 佯谬。
这一现象立刻就被套用到了Rutherford的声电子模型当中，主要研究原子核中的中性粒子（该研究是在中子发现之前）。该佯谬为电子被局域到了原子核中的这一观点提供了一个量子力学争议。该佯谬準确而清晰的指出，电子不会受到原子核中任何势阱的限制。而这一佯谬在当时受到了非常大的争议。
无质量粒子
假设一个无质量的相对论粒子，在一个具有V0的势垒台阶处， 此时E0<V0，动量为p。粒子的波动方程，
， 遵循随时间变化的狄拉克方程：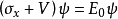
，
，其中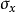
为泡利矩阵，
。
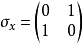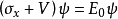
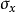
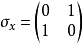
图1
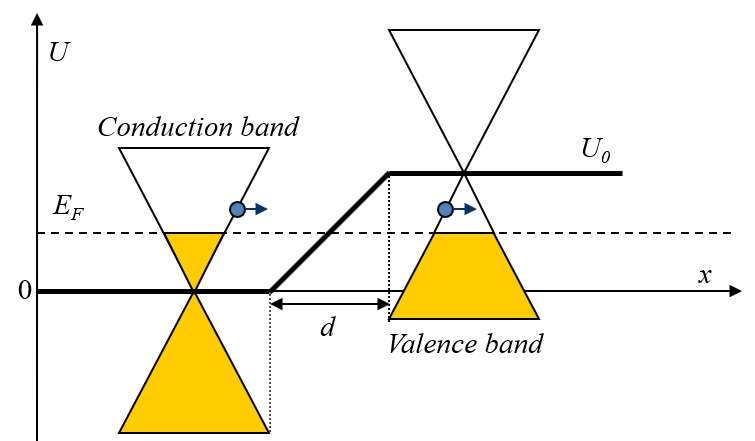
图1假设粒子是由左边开始传播，将遇到两种情况，如图1。
（一） 在台阶之前，在区域1中；
（二） 在势垒中，在区域2中。
则：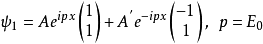
，
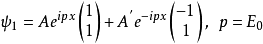
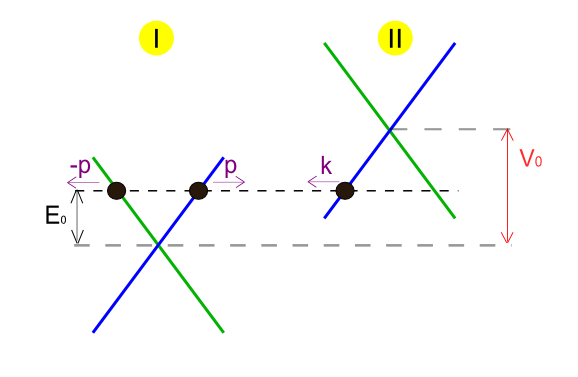图2. 对于色散关係的描述，其中横轴代表动量，纵轴代表能量。其中係数A，A’，和B均为複数。传入与传输波函式均与正群速相关，即图2中蓝色线；而反射波函式则与负群速相关，图2中绿色线。
现在我们预计算传输与反射係数，T,R。它们分别来源于机率振幅电流。而机率电流的定义与狄拉克方程相关：
，
在这一情况下，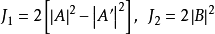
，
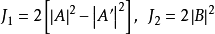
传输与反射係数为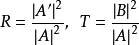
，
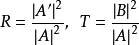
考虑到波函式在x=0时的连续性，则：
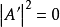
因此传输係数为1，没有反射发生。
Klein隧穿的一个解释为势垒台阶不能改变无质量相对论粒子中群速的方向，这一解释非常符合上述单子粒子的情况。另外，其他文献中较为複杂的解释为在量子场理论的情况下，由于势垒出粒子与反粒子对的存在，将会出现无穷大隧穿。
有质量情况
对于有质量粒子来说，计算与上述无质量粒子类似，结果同样与无质量粒子一样令人惊讶。传输係数始终是大于零的，且接近1时势垒台阶将趋于无穷大。
假如粒子的能量範围处于
，那幺粒子的反射将大于整体反射。
其他情况
这些结果也扩展到了更高的维度、以及其他不同形式的势垒当中，如线台阶、方势垒、光滑势垒、等。一些石墨烯的电子传输实验当中也依赖于Klein隧穿。