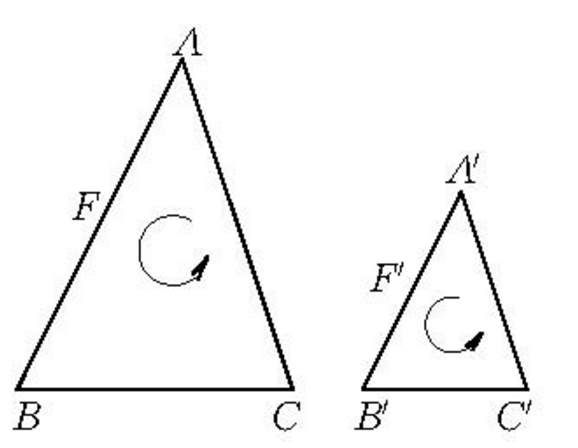
真正相似(true similar)亦称直接相似、同向相似或本质相似，是一种特殊相似形。一个平面到自身的变换，如果对于任意两点A，B，以及对应点A'，B'，总有A'B'=k.AB（k为正实数），那幺，这个变换叫做相似变换，实数k叫做相似比，相似比为k的相似变换常记为H(k)，显然，当k=1时，H(1)就是契约变换。在相似变换下，点A变为点A'，图形F变为图形F'，此时，称F，F'是相似图形，记为F∽F'。与契约图形类似，如果在两个相似图形上，每两个对应三角形沿周界环绕方向相同，则称这两个图形真正相似；如果对应三角形沿周界环绕方向相反，那幺称这两个图形镜像相似。
基本介绍
- 中文名：真正相似
- 外文名：true similar
- 别称：直接相似、同向相似或本质相似
- 所属学科：数学
- 所属问题：平面几何(比例与相似形)
基本介绍
真正相似是一种特殊相似形，设图形F与F′是相似形，在图形F上任取不共线 三点A，B，C，它们在图形F′上的对应点分别是A′，B′，C′(如图1)，若△ABC和△A′B′C′的方向相同，即三对对应点的排列(沿周界ABCA与A′B′C′A′的环绕方向)或同为顺时针方向或同为逆时针方向，则称图形F与图形F′真正相似。真正相似图形的重要特例是真正相似三角形。当△ABC与△A′B′C′相似，且沿周界ABCA与沿周界A′B′C′A′的环绕方向相同，即同为逆时针方向或同为顺时针方向，则这两个三角形是真正相似三角形。
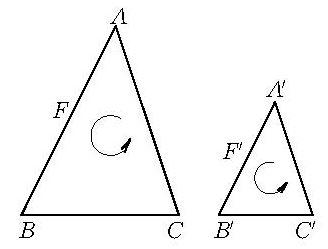图1相关定理
定理1 位似图形必彼此真正相似。
定理2 若两非契约的真正相似图形有一双对应直线互相平行或重合，则它们必是位似图形。
注 必须注意，即使两真正相似图形的每双对应顶点连线共点，但这两图形未必是位似的，例如在下图中所绘的△ABC与△A'B'C'，它们不但真正相似，且有透视中心O，然而它们明明就不是位似图形。
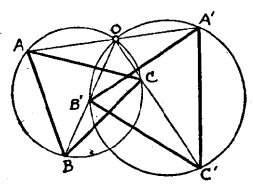图2定理3 既不契约也不位似的两个真正相似图形，可以接连行一次位似变换和一次旋转将其一形变为他形， 其中相似中心和旋转中心是同一点。
定理4设图形F与F'真正相似但不契约，A与A'是任一双对应点，k是相似比。若内外分钱段AA'于M、N，使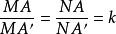
，则直径为MN的圆恆过一定点。
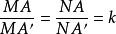
定理5 非契约的两个镜象相似图形，可以接连行一 次反射和一次位似变换将其一形变为另一形，其中反射轴通过相似中心。
定理6 非契约的两个镜象相似图形的两条二重线，内外分每双对应点的连线线所得的分比，都等于两形的相似比。
相关介绍
如果二图形F和F'的点与点之间建立这样的一一对应应关係，即图形F'上任意二点连线而成的线段与图形F上与前二点对应的二点连线而成的线段的比有同一数值，就说图形F'相似子图形F，设A、B、C、D、…为图形F上的点，图形F'上的对应点为A'、B'、C'、D'、…，由定义，必有K=A'B'：AB=A'C'：AC=B'C'：BC=A'D'：AD…=常数，这个比例常数K称为图形F'对于图形F的相似係数或称相似比。
特别地，如果两个边数相同的多边形的对应角都相等，对应边都成比例，这两个多边形叫做相似多边形。对于两个三角形，如果对应角相等，对应边成比例，这两个三角形叫做相似三角形，相似用符号“∽”表示，读作“相似于”。
有两种相似图形。如果给图形以定向， 则有
(1)两相似图形上的每两个对应三角形有同一的定向，每两对应角有同向，这两个相似图形称为真正相似(图3)。
图3(2)两相似图形上的每两个对应三角形有相反的定向，每两对应角有相反方向，这两个相似图形称为镜象相似(图4)。
图4