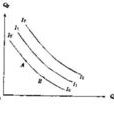
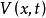比较原理(Comparison Principle)是通过比较微分方程右端直接判断系统稳定性的一种原理。描述系统动力学特性的微分方程之右端是一个函式,由该函式值的大小可判定方程解的大小,从而可用于判别系统运动的有界性和稳定性。
基本介绍
- 中文名:比较原理
- 外文名:comparison principle
- 套用学科:数学术语
- 範畴:数理科学
- 定义:比较微分方程右端判断系统稳定性
- 涉及:系统动力学
微分方程的比较原理
考虑微分方程
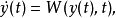


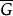
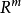
由微分方程解的存在性定理知,任取 ,存在方程
,存在方程 的解
的解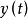 满足
满足 ,记为
,记为 ,并称其为过点
,并称其为过点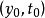 的解。但一般
的解。但一般 不是唯一的,这些解或者在整个区间
不是唯一的,这些解或者在整个区间 上存在,或者于某个有限时间
上存在,或者于某个有限时间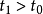 离开
离开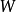 的定义域。如果对向量
的定义域。如果对向量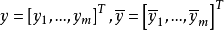 ,用
,用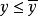 表示
表示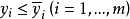 ,则有以下右行最大解的定义。
,则有以下右行最大解的定义。


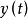


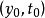


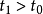
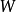
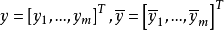
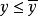
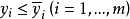
定义:设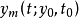 是方程
是方程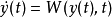 的在区间
的在区间 上有定义且过点
上有定义且过点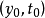 的解,若对此方程的任一个在区间
的解,若对此方程的任一个在区间 上有定义且过点
上有定义且过点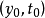 的解
的解 均有
均有
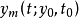
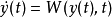

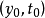

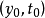

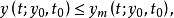
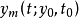
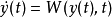

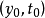
关于右行最大解的存在性,有以下定义。
定义:若定义在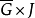 上的一个向量函式
上的一个向量函式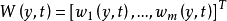 的每个分量
的每个分量 均满足:当任意两向量
均满足:当任意两向量 和
和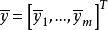 满足
满足 且
且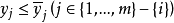 时,不等式
时,不等式 均成立,则称
均成立,则称 是对
是对 拟单调不减的。
拟单调不减的。
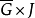
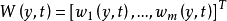


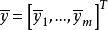

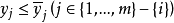



比较原理在稳定性分析中的套用
研究系统
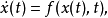
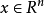

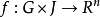

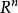
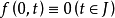
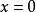
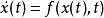

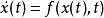
利用比较原理可将判定 维系统
维系统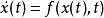 零解稳定性的问题转化为判定一
零解稳定性的问题转化为判定一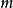 维比较方程零解的稳定性问题。
维比较方程零解的稳定性问题。

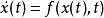
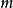
定理:对于系统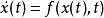 ,若存在向量函式
,若存在向量函式 满足:
满足:
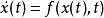

1、 ;
;

2、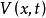 各分量均连续,对
各分量均连续,对 满足局部的
满足局部的 条件,且
条件,且 在
在 中正定。
中正定。