从研究两个质点在万有引力作用下的运动规律出发,人们通常把太空飞行器达到环绕地球、脱离地球和飞出太阳系所需要的最小发射速度,分别称为第一宇宙速度、第二宇宙速度和第三宇宙速度。
第一、二、三宇宙速度分别为
7.9km/s ,11.2km/s ,16.7km/s
基本介绍
- 中文名:三大宇宙速度
- 外文名:cosmic speed limit
- 套用学科:物理
- 适用领域範围:航天学
定义
从研究两个质点在万有引力作用下的运动规律出发,人们通常把太空飞行器达到环绕地球、脱离地球和飞出太阳系所需要的最小发射速度,分别称为第一宇宙速度、第二宇宙速度和第三宇宙速度。
第一宇宙速度
太空飞行器沿地球表面作圆周运动时必须具备的发射速度,也叫环绕速度,以下记为v1。按照力学理论可以计算出v1=7.9公里/秒。但在精确计算中,太空飞行器在距离地面表面数百公里以上的高空运行,地球对太空飞行器引力比在地面时要略小,故其速度也略小于v1。
v1计算
记第一宇宙速度为v1,设地球质量为M,卫星质量为m,地球半径为R,万有引力常数G,地球表面重力加速度g。在以地球为半径的轨道上运行的速度,万有引力=向心力。其中,由于近地,万有引力也可以表示为mg,即
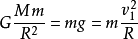
得
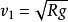
其中,取  ;
; 


得

第二宇宙速度
当太空飞行器超过第一宇宙速度v1达到一定值时,它就会脱离地球的引力场而成为围绕太阳运行的人造行星,这个速度就叫做第二宇宙速度,亦称脱离速度。所谓摆脱地球束缚,就是几乎不受地球引力影响,这与处于离地球无穷远点的位置得情况等价。这里要注意,由于月球还未超出地球引力的範围,故从地面发射探月太空飞行器,不需要达到第二宇宙速度v2,实际上其初始速度不小于10.848 km/s 即可。
v2计算
记第二宇宙速度为v2,设地球质量为M,卫星质量为m,地球半径为R,万有引力常数G,地球表面重力加速度g。发射后全部动能转化为引力势能使卫星跑到离地球无穷远处(机械能守恆)。
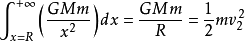
而
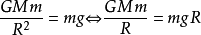
即

故
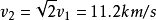
第三宇宙速度
从地球表面发射太空飞行器,飞出太阳系,到浩瀚的银河系中漫游所需要的最小发射速度,就叫做第三宇宙速度。亦称逃逸速度。按照力学理论可以计算出第三宇宙速度V3=16.7公里/秒。需要注意的是,这是选择太空飞行器入轨速度与地球公转速度方向一致时计算出的V3值;如果方向不一致,所需速度就要大于16.7公里/秒了。可以说,太空飞行器的速度是挣脱地球乃至太阳引力的唯一要素,目前只有火箭才能突破该宇宙速度。
v3计算
能脱离太阳的引力到达无穷远处的最小速度。这样只需把第二宇宙速度方程中地球的质量换成太阳的质量,地球半径换成地球公转轨道半径就行了。但不同的是,解出速度后,还要再减去地球的公转速度才是最终的第三宇宙速度;因为地球的公转已经提供了一定的动能了,况且发射速度都是相对于地球来说的。
以离太阳表面无穷远处为0势能参考面,则有(不考虑地球引力)

(vRE为人造天体对太阳的速度,m为人造天体的质量,R为平均日地距离,M为太阳质量)
解得 。
。

由v地球绕太阳=29.8km/s
知v’=42.2-29.8=12.4km/s
设R'为地球半径,M'为地球质量
又由于发射时必须克服地球引力做功,故由机械能守恆定律有
1/2mv1-GM'm/R‘=1/2mv’1
∵GM'm/R'=1/2mv21(v2为第二宇宙速度)
∴1/2mv1-1/2mv21=1/2mv’1
解得v=(v21+v'1)1/2=16.7km/s
三大宇宙速度与人造卫星的发射
当发射速度V与宇宙速度分别有如下关係是,被发射物体的情况将有所不同:
第一种情况,当v<v1时,被发射物体最终仍将落回地面;
第二种情况,当v1≤v<v2时,被发射物体将环绕地球运动,成为地球卫星;
第三种情况,当v2≤v<v3时,被发射物体将脱离地球束缚,成为环绕太阳运动的“人造行星”;
第四种情况,当v≥v3时,被发射物体将从太阳系中逃逸。
由此可见,三个宇宙速度均是发射卫星过程中的不同临界状态。

