矩阵行列式(determinant of a matrix)是指矩阵的全部元素构成的行列式,设A=(aij)是数域P上的一个n阶矩阵,则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。若A,B是数域P上的两个n阶矩阵,k是P中的任一个数,则|AB|=|A||B|,|kA|=kn|A|,|A*|=|A|n-1,其中A*是A的伴随矩阵;若A是可逆矩阵,则|A-1|=|A|-1。
基本介绍
- 中文名:矩阵行列式
- 外文名:determinant of a matrix
- 所属学科:数学
- 所属问题:高等代数(矩阵)
- 简介:矩阵的全部元素构成的行列式
基本介绍
一个n×n的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:
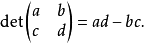
把一个n阶行列式中的元素aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素aij的余子式,记作Mij。记Aij=(-1)i+jMij,叫做元素aij的代数余子式。例如:
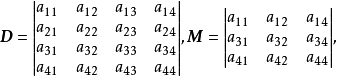
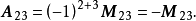
一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即:
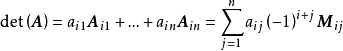
相关定理
定理1 设A为一n×n矩阵,则det(AT)=det(A)。
证 对n採用数学归纳法证明。显然,因为1×1矩阵是对称的,该结论对n=1是成立的。假设这个结论对所有k×k矩阵也是成立的,对(k+1)×(k+1)矩阵A,将det(A)按照A的第一行展开,我们有:
det(A)=a11det(M11)-a12det(M12)+-…±a1,k+1det(M1,k+1),
由于Mij均为k×k矩阵,由归纳假设有
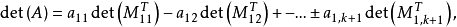
此式右端恰是det(AT)按照AT的第一列的余子式展开。因此
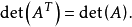
定理2 设A为一n×n三角形矩阵。则A的行列式等于A的对角元素的乘积。
根据定理1,只需证明结论对下三角形矩阵成立。利用余子式展开和对n的归纳法,容易证明这个结论。
定理3 令A为n×n矩阵。
(i) 若A有一行或一列包含的元素全为零,则det(A)=0。
(ii) 若A有两行或两列相等,则det(A)=0。
这些结论容易利用余子式展开加以证明。

