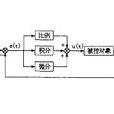
比例积分微分控制,简称PID控制,是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛套用于工业过程控制,至今仍有90%左右的控制迴路具有PID结构。
简单的说,根据给定值和实际输出值构成控制偏差,将偏差按比例、积分和微分通过线性组合构成控制量,对被控对象进行控制。常规PID控制器作为一种线性控制器。
基本介绍
- 中文名:比例积分微分控制
- 外文名: proportional-integral-derivative control
- 简称:PID控制
- 学科:自动化控制
- 释义:按偏差的比例、积分、微分控制
- 特点:算法简单、鲁棒性好、可靠性高
理论简介
经典控制理论在实际控制系统中的典型套用就是PID控制器。在早期的控制系统中,PID控制也是唯一的自动控制方式。伴随着计算机技术的发展,现代控制理论在实用性方面获得了很大进展,解决了许多经典控制理论不能解决的问题。这一现象使很多人认为,新的理论和技术可以取代PID控制。但后来的发展说明,PID控制并没有让位。目前,PID控制仍然是在工业控制中套用得最为广泛的一种控制方法。其原因是:(1)其结构简单,鲁棒性和适应性较强;(2)其调节整定很少依赖于系统的具体模型;(3)各种高级控制在套用上还不完善;(4)大多数控制对象使用常规PID控制即可以满足实际的需要;(5)高级控制难以被企业技术人员掌握。
但由于实际对象通常具有非线性、时变不确定性、强干扰等特性,套用常规PID控制器难以达到理想的控制效果;在生产现场,由于参数整定方法繁杂,常规PID控制器参数往往整定不良、性能欠佳。这些因素使得PID控制在複杂系统和高性能要求系统中的套用受到了限制。
控制原理
常规PID控制系统原理如图1所示,这是一个典型的单位负反馈控制系统。系统由PID控制器和被控对象组成。 图1 PID控制系统原理框图
图1 PID控制系统原理框图
 图1 PID控制系统原理框图
图1 PID控制系统原理框图控制规律
PID控制器是一种线性控制器,它根据给定值r(t)与实际输出值c(t)构成偏差:e(t)=r(t)-c(t)。将偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量,对受控对象进行控制。其控制规律为:

传递函式为: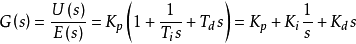 ,式中,Kp为比例係数,Ti为积分时间常数,Td为微分时间常数;Ki=Kp/Ti,为积分係数;Kd=Kp*Td,为微分係数。
,式中,Kp为比例係数,Ti为积分时间常数,Td为微分时间常数;Ki=Kp/Ti,为积分係数;Kd=Kp*Td,为微分係数。
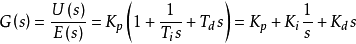
各环节作用
PID控制器各校正环节的作用如下:
比例环节:即时成比例地反应控制系统的偏差信号e(t),偏差一旦产生,控制器立即产生控制作用以减小误差。当偏差e=0时,控制作用也为0。因此,比例控制是基于偏差进行调节的,即有差调节。
积分环节:能对误差进行记忆,主要用于消除静差,提高系统的无差度,积分作用的强弱取决于积分时间常数Ti,Ti越大,积分作用越弱,反之则越强。
微分环节:能反映偏差信号的变化趋势(变化速率),并能在偏差信号值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减小调节时间。
从时间的角度讲,比例作用是针对系统当前误差进行控制,积分作用则针对系统误差的历史,而微分作用则反映了系统误差的变化趋势,这三者的组合是“过去、现在、未来”的完美结合。
性能指标
衡量一个PID控制系统性能好坏的指标主要有:上升时间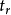 、超调量
、超调量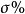 、调节时间
、调节时间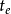 和稳态误差
和稳态误差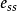 。其中:
。其中:
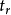
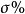
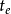
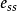
(1)上升时间 是指系统实际输出从正常输出的10%上升到正常输出的90%时所需的时间;
是指系统实际输出从正常输出的10%上升到正常输出的90%时所需的时间;

(2)调节时间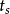 是指系统实际输出值稳定在正常输出值的5%或2%範围以内时所需的时间;
是指系统实际输出值稳定在正常输出值的5%或2%範围以内时所需的时间;
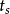
(3)超调量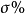 是指系统实际输出的最大值与正常值的差与正常值的比值;
是指系统实际输出的最大值与正常值的差与正常值的比值;
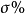
(4)稳态误差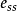 是指系统达到稳态时的输出值与正常值差的绝对值与正常值的比值。
是指系统达到稳态时的输出值与正常值差的绝对值与正常值的比值。
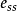
这四个参数反映了系统的回响能力和稳定性,通过它们就可以判定一个系统性能的好坏。
参数选取
长期以来,在设计和套用PID控制器的过程中,PID参数的选取一直是一个难题,这是因为:
(1)比例作用使得控制器的输入输出成比例关係,为了儘量减小偏差,同时也为了加快回响速度,缩短调节时间,就需要增大Kp。但比例作用过大会使系统动态性能变坏,甚至会使闭环系统不稳定。
(2)积分作用的引入有利于消除稳态误差,但使系统的稳定性下降。尤其在大偏差阶段的积分往往会使系统产生过大的超调,调节时间变长。
(3)微分作用的引入使系统能够根据偏差变化的趋势做出反应,适当的微分作用可加快系统回响,有效地减小超调,改善系统的动态特性,增加系统的稳定性。不利之处是微分作用对干扰敏感,使系统抑制干扰能力降低。
因此,PID控制器的参数选取必须兼顾动态与静态性能指标要求,只有合理地整定Kp、Ki、Kd三个参数,才能获得比较满意的控制性能。
整定方法
所谓PID控制器参数整定就是设定和调整控制器的参数,使控制系统的过渡过程达到满意的品质。参数整定方法主要有以下几类:基于被控过程对象参数辨识的整定方法,这种方法首先要辨识出对象的参数模型,再利用极点配置整定法、相消原理法等理论计算整定法整定;基于抽取对象输出回响特徵参数整定法,如Z-N参数整定法(也称临界比例度法);参数最佳化方法;基于模式识别的专家系统法以及基于控制器自身控制行为的控制器参数线上整定方法。下面介绍几种常用的整定方法。
凑式法
所谓凑试法是先将调节器的参数根据经验设定在某一数值上,然后在闭环系统中加扰动,观察过渡过程的曲线形状,若曲线不够理想,则以调节器P、I、D参数对系统过渡过程的影响为依据,按照先比例,后积分,最后微分的顺序,将调节器参数逐个进行反覆凑试,知道获得满意的控制质量。
具体步骤如下:
(1)置调节器积分时间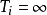 ,微分时间
,微分时间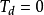 ,在比例度
,在比例度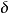 按经验设定的初始条件下,将系统投入运行,整定比例度
按经验设定的初始条件下,将系统投入运行,整定比例度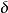 。若曲线振荡频繁,则加大比例度
。若曲线振荡频繁,则加大比例度 ;若曲线超调量大,且趋于非周期过程,则减小比例度
;若曲线超调量大,且趋于非周期过程,则减小比例度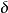 ,求得满意的4:1过渡过程曲线。
,求得满意的4:1过渡过程曲线。
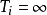
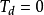
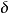
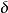

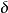
(2)引入积分作用〔此时将上述比例度 增大1.2倍〕。将界由大到小进行整定。若曲线波动较大,则应增大积分时间
增大1.2倍〕。将界由大到小进行整定。若曲线波动较大,则应增大积分时间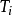 ;若曲线偏离给定值后长时间回不来,则需减小
;若曲线偏离给定值后长时间回不来,则需减小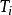 ,以取得较好的过渡过程曲线。
,以取得较好的过渡过程曲线。

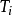
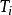
(3)若需引入微分作用,则将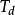 按经验值或按
按经验值或按 设定,并由小到大加入。若曲线超调量大而衰减慢,则需增大
设定,并由小到大加入。若曲线超调量大而衰减慢,则需增大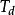 ;若曲线振荡厉害,则应减小
;若曲线振荡厉害,则应减小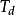 。观察曲线,适当调整比例度
。观察曲线,适当调整比例度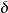 和
和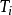 ,直到求得满意的过渡过程曲线。
,直到求得满意的过渡过程曲线。
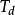

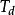
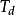
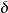
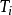
临界比例度法(Z-N法)
本方法是由齐格勒(Ziegler)和尼柯尔斯(Nichols)提出的一种PID参数工程整定方法。这种方法是基于闭环回响的方法,在闭合的控制系统里,将调节器置于纯比例作用下,从大到小逐渐改变调节器的比例度,得到等幅振荡的过渡过程,此时的比例度称为临界比例度,用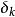 表示,相邻两个波峰间的时间间隔,称为临界振荡周期,用
表示,相邻两个波峰间的时间间隔,称为临界振荡周期,用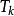 表示,通过计算即可求出调节器的整定参数。这种方法基于频率回响的分析。其步骤如下:
表示,通过计算即可求出调节器的整定参数。这种方法基于频率回响的分析。其步骤如下: 图2
图2
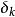
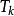
 图2
图2(1)将调节器的积分时间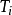 置于最大(
置于最大( ),微分时间
),微分时间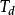 置零(
置零(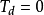 ),比例度
),比例度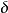 适当,将系统投入运行。
适当,将系统投入运行。
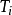

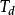
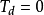
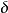
(2)将比例度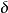 逐渐减小,得到等幅振荡过程,记下临界比例度
逐渐减小,得到等幅振荡过程,记下临界比例度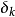 和临界振荡周期
和临界振荡周期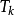 值。
值。
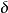
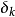
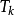
(3)根据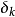 、
、 值,採用图2中的经验公式,计算出调节器各个参数,即
值,採用图2中的经验公式,计算出调节器各个参数,即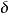 、
、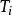 、
、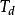 的值。
的值。
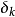

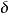
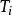
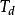
衰减曲线法
衰减曲线法是在总结临界比例度法的基础上,经过反覆实验提出来的。其具体的整定步骤如下(以4:1衰减过程为例,10:1衰减过程类似): 图3
图3
 图3
图3(1)先把过程控制系统中调节器参数置成纯比例作用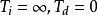 ,使系统投入运行,再把比例度
,使系统投入运行,再把比例度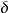 从大到小逐渐调小,直到出现所要求的4:1衰减过程曲线,此时的比例度为4:1衰减比例度
从大到小逐渐调小,直到出现所要求的4:1衰减过程曲线,此时的比例度为4:1衰减比例度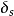 ,两个相邻波峰间的间隔称为4:1衰减振荡周期
,两个相邻波峰间的间隔称为4:1衰减振荡周期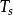 。
。
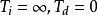
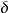
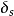
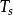
2、根据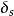 、
、 使用图3所示公式,即可计算出调节器的各整定参数值。
使用图3所示公式,即可计算出调节器的各整定参数值。
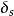

3、按“先P后I最后D”的操作程式,将所求得的整定参数设定在调节器上。再观察运行曲线,若不太合理,可做适当调整。
以上介绍了几种常用的PDI控制器参数整定方法,除上述方法外,还有多种整定方法,如过程反应曲线法,又称C-C法:继电型PID自整定方法,它的基本思想是在控制系统中设定两种模态:测试模态和调节模态。在测试模态,由一个继电非线性环节来测试系统的振荡频率和增益,而在调节模态下,由系统的特徵参数首先得出PID控制器,再通过此控制器调节系统的动态性能。如果系统的测试发生变化,则需要重新进入测试模态进行测试,测试完成之后在回到调节模态进行控制;此外,还有基于增益最佳化的整定法、基于总和时间常数的整定法和基于交叉两点法、ISTE最优设定法等。