正锥是偏序群的正元素集,若G是偏序群,则G的正元素集G+={g∈G|g>0}及G的负元素集G-={g∈G|g<0}分别称为G的正锥及负锥。G+满足三个条件: 1.G++G+⊆G+;2.G+∩-G+=G+∩G-={0};3.对任意a∈G有a+G+-a⊆G+。反之,若P是群G的子集,G的运算记为+,且P满足条件1、2、3,对任意x,y∈G,定义x>y若且唯若x-y∈P,则由P可诱导出G的一个序,使G成为偏序群,且P=G+,于是,一个偏序群的序完全由满足上述条件的子集P所确定,因此,亦称P是G的一个序。
基本介绍
- 中文名:正锥
- 外文名:positive cone
- 所属学科:数学
- 相关概念:偏序群、序关係、凸映射等
基本介绍
在给定的线性空间中,可以引进一个凸锥来规定一种序关係。这是讨论线性空间中不等式关係的一个必不可少的前提。
定义 设X是一个线性空间,P足X中的一个凸锥,并且对于任意的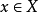 与
与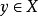 ,若
,若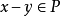 ,则记为
,则记为 。对于这样的P称为X中的一个正凸锥,有时简称为正锥;若令
。对于这样的P称为X中的一个正凸锥,有时简称为正锥;若令 ,则称N为X中的负凸锥,简称为负锥。显然,若
,则称N为X中的负凸锥,简称为负锥。显然,若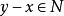 ,则有
,则有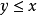 。
。
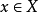
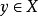
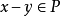


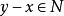
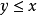
例如,在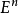 中凸锥
中凸锥
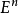
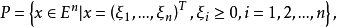
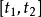
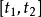
正锥与凸映射
很容易验证,上述定义中的序关係,满足以下三条性质:
1.自反性 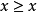 。
。
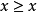
2.传递性 若 ,又
,又 ,则
,则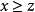 。
。


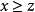
3.对称性 若 ,又
,又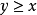 ,则
,则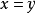 。
。

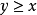
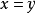
如果在X中定义了序关係“≥”,并且满足上述三条公理,那幺就称在X中用正锥P定义了偏序关係。对于偏序关係我们需注意,在X中并非任意两个元素都是可比的,所以才称之为偏序。
在赋范线性空间中,有时用闭凸锥来定义正锥具有特殊的意义。另外,如果x是正锥P的一个内点,那幺可以把它记为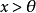 。对于许多套用问题,为了能够使用凸集分离定理,P至少要有一个内点,这是必不可少的条件。
。对于许多套用问题,为了能够使用凸集分离定理,P至少要有一个内点,这是必不可少的条件。
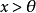
给定一个赋范线性空间X与一个正凸锥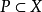 ,还可以在其对偶空间X*中定义一个对应的对偶正凸锥
,还可以在其对偶空间X*中定义一个对应的对偶正凸锥
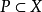

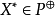
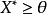
即使P不一定是闭的,而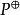 却总是闭的。如果P是闭的,那幺在P与
却总是闭的。如果P是闭的,那幺在P与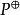 之间有下列关係:
之间有下列关係:
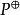
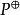
命题1 设X是一个赋范线性空间,P是X中的正凸锥,并且P是闭的。若x∈X,对于所有的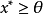 ,满足
,满足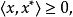 则
则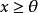 。
。
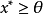
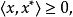
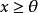
证明: 用反证法假设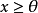 不成立,即
不成立,即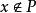 ,那幺根据凸集分离定理,即知存在一个闭超平面,亦即有界线性泛函
,那幺根据凸集分离定理,即知存在一个闭超平面,亦即有界线性泛函 ,使得对于所有的p∈P,由于P是闭的,应有
,使得对于所有的p∈P,由于P是闭的,应有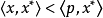 。由于P是X中的凸锥,所以
。由于P是X中的凸锥,所以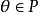 ,所以特别有
,所以特别有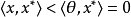 ,此与命题之假设不符。故必有
,此与命题之假设不符。故必有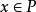 ,即
,即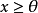 。
。
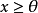
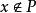

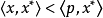
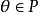
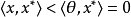
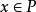
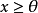
命题2 设X是一个赋范线性空间,P是X中的正凸锥,若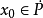 ,则对于所有非零的
,则对于所有非零的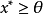 ,有
,有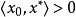 。
。
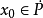
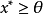
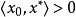
证明:由于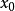 是P的内点,所以存在一个以
是P的内点,所以存在一个以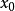 为中心,以r>o为半径的闭球
为中心,以r>o为半径的闭球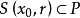 ,即当
,即当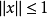 时,有
时,有 。由于
。由于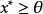 ,所以
,所以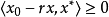 ,即
,即 。从而根据範数的定义,有
。从而根据範数的定义,有
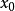
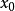
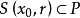
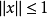

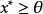
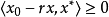

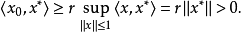
以上,我们已经推广了向量不等式的概念,这就有可能使我们引进关于映射的凸性定义。
定义 设X是一个线性空间,Z也是一个线性空间,在Z中具有正凸锥P。若映射 ,G的定义域是Ω,Ω是X中的凸集,并且对于所有的x1,x2∈Ω以及α∈ [0,1],有
,G的定义域是Ω,Ω是X中的凸集,并且对于所有的x1,x2∈Ω以及α∈ [0,1],有

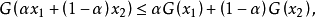
则称G是一个凸映射。

