在泛函分析中，哈恩-巴拿赫定理是一个极为重要的工具。它允许了定义在某个向量空间上的有界线性运算元扩张到整个空间，并说明了存在「足够」的连续线性泛函，定义在每一个赋范向量空间，使对偶空间的研究变得有趣味。这个定理以汉斯·哈恩和斯特凡·巴拿赫命名，他们在1920年独立证明了这个定理。
基本介绍
- 中文名：哈恩一巴拿赫定理
- 外文名：Hahn-Banach theorem
- 套用学科：数学
- 适用领域範围：函式
哈恩一巴拿赫定理(Hahn-Banach theorem)线性函式的延拓定理.哈恩一巴拿赫定理是线性泛函分析的基本定理，但它实际上与凸集分离定理等价，因而也可看做凸集分离定理的解析形式一般的哈恩-巴拿赫定理可以这样来叙述:
定理：设X为实线性空间，M为它的线性子空间，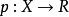
是X上的次可加正齐性泛函，
是M上的线性泛函，则
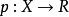
（1）存在X上的线性泛函
使得
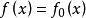，任意的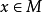
.
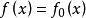
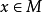
（2）若
，则可使
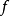满足
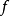
一般泛函分析教科书中的X常取为赋范线性空间，p则取为空间的範数.这样，哈恩一巴拿赫定理就变为线性泛函的保持範数不变的可延拓定理
前面已经提到，从选择公理可以推出哈恩-巴拿赫定理。然而，反过来不成立。注意超滤子引理比选择公理更弱，但从它也可以推出哈恩-巴拿赫定理（反过来则不行）。实际上，哈恩-巴拿赫定理还可以用比超滤子引理更弱的假设来证明。
对于可分空间|可分巴拿赫空间，Brown和Simpson证明了哈恩-巴拿赫定理可以从WKL0——一个二阶算术的弱子系统推出。