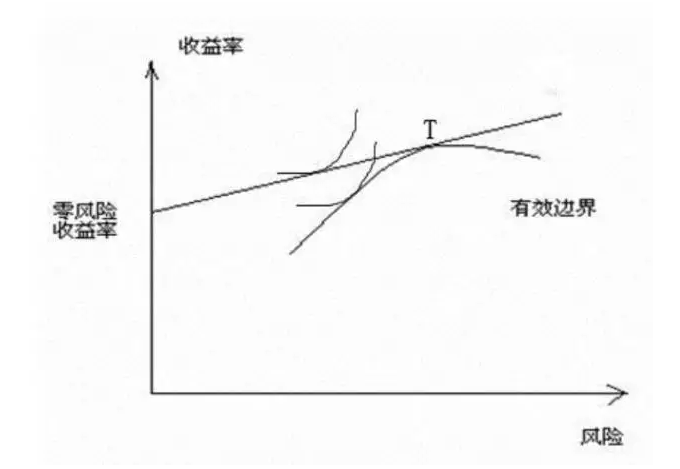
凸集分离定理是凸集理论的最基本的定理,它是指在很弱的条件下,两个不相交的凸集总可用超平面分离。
基本介绍
- 中文名:凸集分离定理
- 外文名:Separating Hyperplane Theorem
- 别称:超平面分离定理
- 套用学科:物理
- 两个凸集分离:两个凸集合没有交叉和重合的部分
- 範数的等价性:这里的範数可以是任何一种範数
定义
凸集分离定理(超平面分离定理)是套用凸集到最最佳化理论中的重要结果,这个结果在最最佳化理论中有重要的位置。所谓两个凸集分离,直观地看是指两个凸集合没有交叉和重合的部分,因此可以用一张超平面将两者隔在两边。
设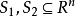 为两个非空集合,如果存在非零向量
为两个非空集合,如果存在非零向量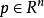 及
及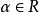 使得
使得
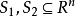
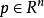
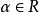
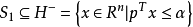

则称超平面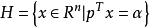 分离了集合
分离了集合 与
与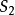 。
。
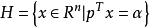

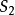
证明
为了证明凸集分离定理,先给出凸集的一个性质,我们不妨把一个闭凸集想像成为一个三维的充满了气体的气球(因为必须是凸的),那幺,在气球外一点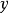 ,到气球内个点
,到气球内个点 (包括内部)的距离是不一样的,但肯定在气球上有一点,它到
(包括内部)的距离是不一样的,但肯定在气球上有一点,它到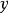 的距离是所有距离中最小的,这是凸集特有的性质。下面是这个性质的定义及证明:
的距离是所有距离中最小的,这是凸集特有的性质。下面是这个性质的定义及证明:
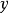

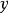
引理
设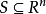 为非空闭凸集,
为非空闭凸集,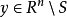 ,则存在唯一的
,则存在唯一的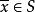 ,使得该点与
,使得该点与 的距离最小,即有:
的距离最小,即有:
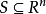
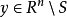
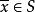

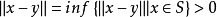
根据範数的等价性,这里的範数可以是任何一种範数。
引理证明
先证明其存在性,考虑单位超球
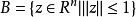
取足够大的正数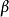 ,使
,使 。
。
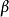

因为 为闭集,而
为闭集,而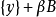 是一个有界闭集,所以
是一个有界闭集,所以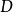 是一个非空有界闭集,于是
是一个非空有界闭集,于是 可以在
可以在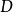 上的某一点取得它的最大值,在另一点上取得其最小值。
上的某一点取得它的最大值,在另一点上取得其最小值。

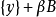
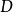

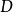
设这个最小值在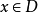 处达到,即
处达到,即 是
是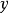 到
到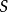 的最小距离点,记此距离值为
的最小距离点,记此距离值为 。
。
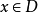

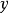
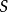

再证唯一性。
假设还存在另一点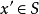 ,使
,使
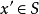
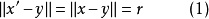
记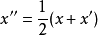 。
。
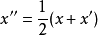
因为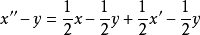 ,两边取範数,则有
,两边取範数,则有
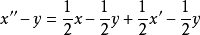
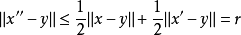
但是由于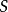 是凸集,
是凸集,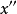 是
是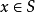 与
与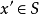 的凸组合,所以
的凸组合,所以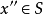 。
。
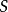
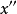
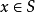
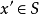
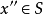
而由于 是
是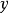 到
到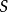 的最小距离,故
的最小距离,故

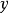
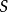
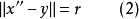
根据平行四边形定律(两对角线的平方和等于一组临边平方和的两倍),有:

把(1)和(2)代入,有
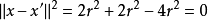
故有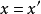 ,唯一性得证。在此基础上,可以给出凸集分离定理的证明。
,唯一性得证。在此基础上,可以给出凸集分离定理的证明。
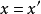
定理证明
因为 为非空集合,
为非空集合,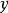 是
是 外的一点,故由引理知,存在一点
外的一点,故由引理知,存在一点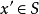 ,使得
,使得

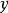

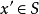
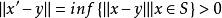
设 ,那幺因
,那幺因 为凸集,故有
为凸集,故有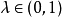 ,使
,使


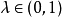
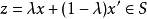
因此,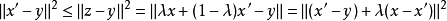
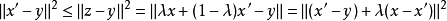
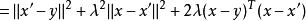
上式两边的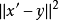 可消去,得
可消去,得
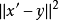
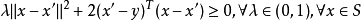
在上式中,令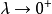 ,得
,得
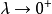
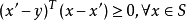
记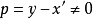 ,有
,有
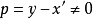
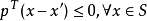
若记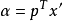 ,则有
,则有
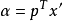

另一方面,由于
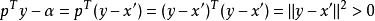
所以

定理得证。
套用
凸集分离定理的一个套用例子是Farkas引理,这个定理是最优性条件中最重要的基础。
利用Farkas引理,还可以证明有价值的Gordan定理和择一性定理。Gorden定理在证明最优性条件中着名的Kuhn-Tucker条件,是极为关键的基础。