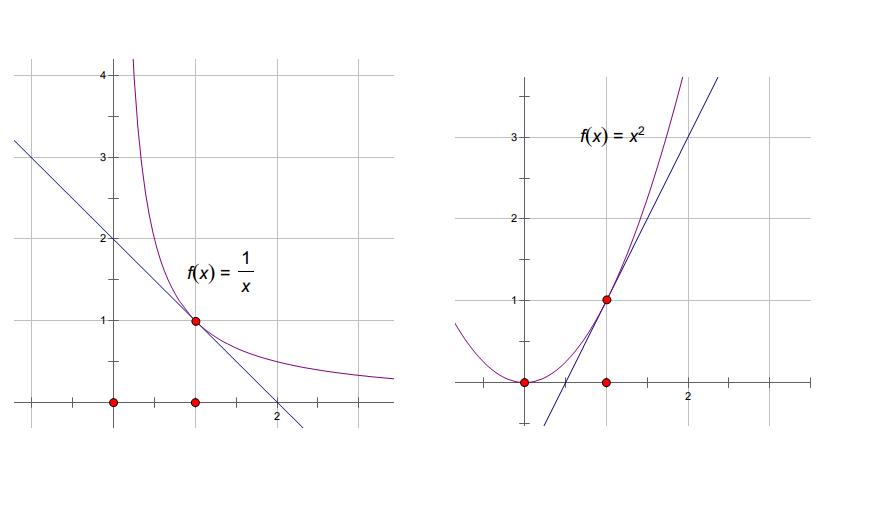
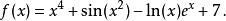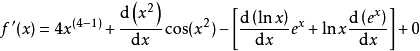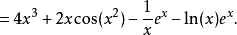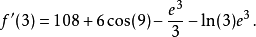导数(英语:Derivative)是微积分学中重要的基础概念。一个函式在某一点的导数描述了这个函式在这一点附近的变化率。导数的本质是通过极限的概念对函式进行局部的线性逼近。当函式f的自变数在一点x0上产生一个增量h时,函式输出值的增量与自变数增量h的比值在h趋于0时的极限如果存在,即为f在x0处的导数。
物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如,导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。
基本介绍
- 中文名:一阶导数
- 外文名:derivative
- 学科:数学
- 别称:变化率
- 性质:数学概念
- 所属领域:数学
- 提出者:莱布尼兹
历史
导数和积分的发现是微积分发明的关键一步。十七世纪以来,光学透镜的设计以及炮弹弹道轨迹的计算促使欧洲的数学家对曲线的切线进行研究。1630年代,法国数学家吉尔·德·罗伯瓦尔作出了最初的尝试。与此同时,同是法国人的费马在计算切线时已经使用了无穷小量的概念。
英国的巴罗、荷兰的于德(Johnann Van Waveren Hudde)和瓦隆的斯卢兹(René Francoiss Walther de Sluze)继续了费马的工作。然而,费马和巴罗等人并没有将求导归纳为一种独立的工具,只是给出了具体的计算技巧。
十七世纪六十年代,英国人伊萨克·牛顿提出了“流数”的概念。牛顿在写于1671年的《流数法与无穷级数》中对流数的解释是:“我把时间看作是连续的流动或增长,而其他的量则随着时间而连续增长。我从时间流动性出发,把所有其他量的增长速度称为流数。”也就是说,流数就是导数。牛顿将无穷小的时间间隔定义为“瞬间”(moment),而一个量的增量则是流数与瞬间的乘积。求导数时,牛顿将自变数和因变数两边展开,同时除以瞬间,再将剩下的项中含有瞬间的项忽略掉。而在他的第三篇微积分论文中,牛顿使用了新的概念:最初比和最后比。他说:随我们的意愿,流数可以任意地接近于在儘可能小的等间隔时段中产生的增量,精确地说,它们是最初增量的最初的比,它们也能用和它们成比例的任何线段来表示。
相比于牛顿,德国数学家莱布尼兹使用了更清晰的记号来描述导数。他利用了巴罗的“微分三角形”概念,将自变数和因变数的增量记为dx和 dy。他把dx理解为“比任何给定的长度都要小”,而dy则是 x 移动时y“瞬刻的增长”。而导数则是两者之间的比例。他还研究了函式之和、差、积、商的求导法则。
微积分的理论面世后,遭到了有关无穷小量定义的攻击与质疑。导数的定义自然也包括在内。莱布尼兹和牛顿对无穷小量的认识都是模糊的。不仅如此,莱布尼兹甚至引入(d)x 和 (d)y,称其为“未消失的量”,用以进行求导前部的计算。在完成计算后再用“消失的量”dx 和dy来代替它们,并假定前两者之比等于后两者之比,认为这是一个不容置疑的真理。
许多数学家,包括伯努利兄弟、泰勒、麦克劳林、达朗贝尔、拉格朗日和欧拉都想要对微积分的严密性辩护或将微积分严密化。但受限于对无穷小量的认识,十八世纪的数学家并没有做出太大的成果。微积分的强烈抨击者,英国的乔治·贝克莱主教在攻击无穷小量时认为,流数实际上是“消失的量的鬼魂”,是0与0之比。欧拉承认后者,并认为0与0之比可以是有限值。拉格朗日则假定函式都可以展开为幂级数,并在此基础上定义导数。
十九世纪后,随着对函式连续性和极限的更深刻认识,微积分终于趋于严谨。波尔查诺是首先将导数定义为函式值的改变数与自变数增量之比在自变数增量无限接近0时趋向的量。波尔查诺强调导数不是0与0之比,而是前面的比值趋向的数。柯西在他的着作《无穷小分析教程概论》中也使用了同样的定义,并定义dy为导数与 dx的乘积。这样,导数和微分的概念得到了统一。
定义
一般定义
设有定义域和取值都在实数域中的函式y=f(x)。若f(x) 在点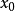 的某个邻域内有定义,则当自变数x在x0处取得增量
的某个邻域内有定义,则当自变数x在x0处取得增量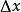 (点
(点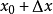 仍在该邻域内)时,相应地y取得增量
仍在该邻域内)时,相应地y取得增量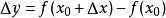 ;如果
;如果 与
与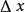 之比当
之比当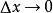 时的极限存在,则称函式y=f(x) 在点
时的极限存在,则称函式y=f(x) 在点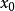 处可导,并称这个极限为函式 y=f(x)在点
处可导,并称这个极限为函式 y=f(x)在点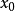 处的导数,记为
处的导数,记为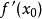 ,即:
,即:
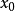
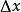
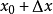
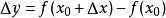

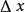
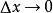
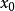
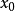
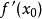
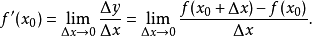

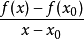

几何意义
当函式定义域和取值都在实数域中的时候,导数可以表示函式的曲线上的切线斜率。如右图所示,设P0为曲线上的一个定点,P为曲线上的一个动点。当P沿曲线逐渐趋向于点P0时,并且割线PP0的极限位置P0T存在,则称P0T为曲线在P0处的切线。
若曲线为一函式y=f(x)的图像,那幺割线PP0的斜率为:

当P0处的切线P0T,即PP0的极限位置存在时,此时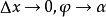 ,则P0T的斜率
,则P0T的斜率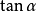 为:
为:
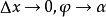
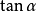
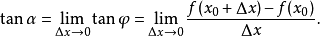
上式与一般定义中的导数定义完全相同,也就是说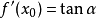 ,因此,导数的几何意义即曲线y=f(x)在点
,因此,导数的几何意义即曲线y=f(x)在点 处切线的斜率。
处切线的斜率。
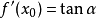

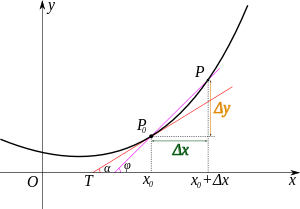 图1.几何意义
图1.几何意义性质
单调性
一阶导数表示的是函式的变化率,最直观的表现就在于函式的单调性定理:设f(x)在[a,b]上连续,在(a,b)内具有一阶导数,那幺: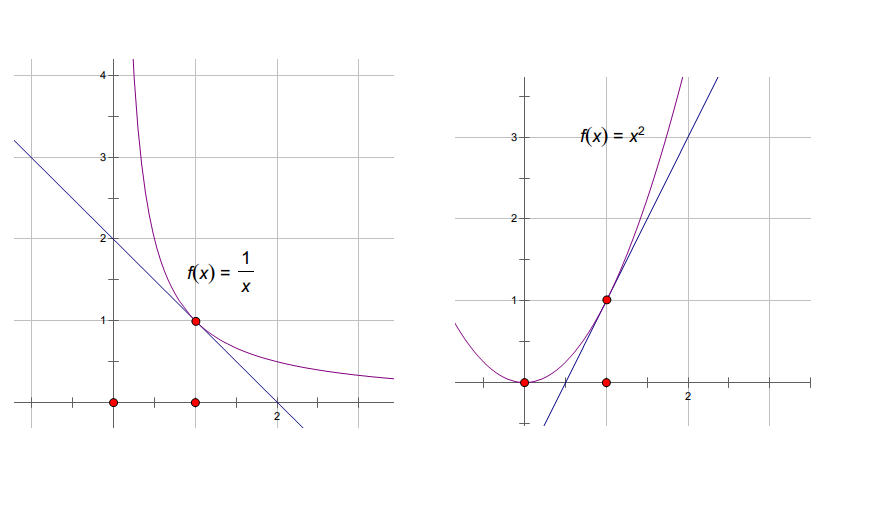 图2.单调性
图2.单调性
 图2.单调性
图2.单调性(1)若在(a,b)内f'(x)>0,则f(x)在[a,b]上的图形单调递增;
(2)若在(a,b)内f’(x)<0,则f(x)在[a,b]上的图形单调递减;
(3)若在(a,b)内f'(x)=0,则f(x)在[a,b]上的图形是平行(或重合)于x轴的直线,即在[a,b]上为常数。
在右图可以直观的看出:函式的导数就是一点上的切线的斜率。当函式单调递增时,斜率为正,函式单调递减时,斜率为负。
导数与微分
微分也是一种线性描述函式在一点附近变化的方式。微分和导数是两个不同的概念。但是,对一元函式来说,可微与可导是完全等价的。可微的函式,其微分等于导数乘以自变数的微分dx,换句话说,函式的微分与自变数的微分之商等于该函式的导数。因此,导数也叫做微商。函式y=f(x)的微分又可记作dy=f'(x)dx。
可导的条件
如果一个函式的定义域为全体实数,即函式在实数域上都有定义,那幺该函式是不是在定义域上处处可导呢?答案是否定的。函式在定义域中一点可导需要一定的条件。首先,要使函式f在一点可导,那幺函式一定要在这一点处连续。换言之,函式若在某点可导,则必然在该点处连续。
可导的函式一定连续,不连续的函式一定不可导。
例子
欲求函式