传统的SISO天线系统中，编码只有时间维度一个自由度可以利用；在MIMO系统中，由于多天线的存在，可以利用空间信道的独立性，来同时获得时间和空间两个自由度，即空时处理技术。多天线系统为提高无线通信的性能提供了一个有效的方法，相比于传统的SISO系统，在频谱效率方面有着明显的优势。一般地，MIMO系统在实际套用中主要有两种实现方式：空间分集（Spatial Diversity）与空间复用（Spatial Multiplexing）。
分集的主要思想就是为接收机提供发射信号的不同副本。若这些副本经历的衰落各自独立，那幺所有这些副本同时经历深度衰落的可能性就很小。因此，接收机能够用这些接收到的信号对发射信号进行可靠的解码。发射信号的副本可以通过不同的手段进行传送。例如，可以在不同的时隙、不同的频率、不同的极化方向或者不同的天线上发射。若不同的时隙用于分集，我们称之为时间分集。当两个时隙之间的间隔大于信息的相干时间，其经历的衰落相互独立。因此，我们可以在这些不连续的时隙上传送不同的副本。但是时间分集由于引入时间冗余，会降低系统总的吞吐率。另一种分集的方法是频率分集。频率分集是利用不同的载波频率来获得分集。当信号的副本间隔大于信道的相干频宽时，信号的副本通过不同的载波频率发射，其经历的信道衰落独立。与时间分集类似，频率分集引入频域冗余，会降低系统的频谱效率。
基本介绍
- 中文名：点对点MIMO技术
- 外文名：Point to point MIMO Technology
- 套用学科：通信
分集与空时编码设计
1.1分集技术
1．时间分集
时间分集是指以超过信道相干时间的时间间隔重複传送信号，以便让再次收到的信号具有独立的衰落环境，从而产生分集效果。相干时间是信道衰落过程相干的时间周期的统计测量值。在数字通信系统中，通常使用差错控制编码以获得相对于未编码系统的编码增益。在移动通信中，一般使用差错控制编码结合交织技术来实现时间分集。在这种情况下，发射分集的副本通常以差错控制编码带来的时域冗余形式到达接收端。由时间交织提供发射信号副本之间的时间间隔，从而在解码器的输入端得到独立的衰落。现在时间分集技术已经被大量地用于扩频CDMA的Rake接收机中，以处理多径信号。时间分集方案由于在时间域上引入冗余，使得频宽的利用率受到损失。
2．频率分集
频率分集方式在多于一个载频上传送信号。这项技术的工作原理是基于在信道相干频宽之外的频率上不会出现同样的衰落。在理论上，不相关信道产生同样衰落的机率是各自产生衰落机率的乘积。在移动通信中，发射信号副本通常按频域冗余的形式到达接收端。这种频域冗余是由直接序列扩频（DSSS）、多载波调製和调频等扩频技术引入的。同时间分集一样，由于在频域上引入的冗余，频率分集也使得频宽的利用率受到损失。
3．空间分集
在使用时间分集时，几个相干时间周期上的交织和编码是十分重要的。当有严格的时延限制或相干时间很大时，就无法实现。因此需要採用其他的分集方案。
天线分集也就是空间分集，通过在传送方和/或接收方放置多个天线来实现，当天线放置的足够远时，不同天线对之间的信道增益差不多独立，同时产生了独立的信号路径。天线距离依赖于当时的散射环境和载波频率。例如移动台接近地面散射丰富时，信道在很短的空间距离下就可以达到不相关，典型的天线间距为半个到一个载波波长。对于位置比较高的基站来说，将需要几个到十几个波长的大的天线距离。
4．接收分集
接收分集是在接收端使用多根天线接收发射信号的独立副本。合理合併发射信号的副本能够降低多径衰落的影响，并且提高总的接收SNR。传统的智慧型天线系统採用最大比合併的方法来提高接收信号质量。接收分集最大的问题在于开销、尺寸和功率较大，有时较难实现。例如在IS-136中，基站端使用多根天线建立上行（从移动台到基站）接收分集，补偿移动台相对较低的发射功率。这样做能够提高上行链路的质量和变化範围。但对下行链路（从基站到移动台）而言，移动台很难使用接收分集。首先，在较小的便携移动台上不便于安装两根以上的天线。其次，多根接收天线意味着要採用多套射频变频器，因此需要更大的处理功率，而移动台功率是受限的。对于下行链路来说，比较实际可行的解决办法是採用发射分集。近年来对发射分集的研究也成为热点。
5．发射分集：空时编码
发射分集的基本思想是通过在接收方採用适当的信号处理技术将传送端的冗余利用起来。现在考虑有L个发射天线和1个接收天线的情况。这在蜂窝系统下行链路中是很普遍的，因为在基站方放置多天线要比在移动台放置多天线要容易的多。它很轻易就能达到分集增益为L，只不过在L个符号间隔内L个不同的天线上传送相同的符号就可以了。在任一时间，只有1个天线传送。这就是简单的重複编码而已，但是，重複编码是非常浪费自由度的。更普遍的方案是把时间分集中的差错控制编码套用到天线分集中。在一个时间段只用一个天线，在不同天线连续传送经过时间分集编码的编码符号，这就是空时编码（STC）的基本思想，这种设计方案带来的好处是：空时码可以在不牺牲频宽的情况下实现发射分集和获得一定的编码增益；空时码还可以和多根接收天线相结合以降低多径衰落的影响，达到MIMO系统的容量。空时码分为空时分组码和空时格线码，这里主要介绍空时分组码。
1.2空时码设计準则
Alamouti码的提出，触发了人们对STC的研究热情。但Alamouti码也有其天然的局限性：如只能用在两个发射天线系统中，不能扩展到更多天线，后续的研究将Alamouti码增强并推广到更多的天线，并由此产生了正交空时编码与準正交空时编码，空时格形码，差分空时编码及其相关增强技术。
空时编码的设计準则：
（1）矩阵秩準则：为了获得最大的分集增益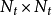
，矩阵误差函式必须满秩。若矩阵误差函式出现秩亏缺，且其秩为r，则空时编码的分集增益为
。
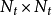
（2）行列式準则：若空时码已经是全分集增益，则其编码增益为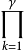
λk，即为矩阵误差函式的行列式的值det[A(C,E)]。
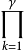
上述两个设计準则为空时编码的设计与分析提供了良好的理论基础，并为后续线性离散码的研究提供了极为重要的设计参考。
空分复用技术
空间复用就是在接收端和发射端使用多副天线，充分利用空间传播中的多径分量，在同一频带上使用多个数据通道（MIMO子信道）发射信号，从而使得容量随着天线数量的增加而线性增加。因此它在概念上是不同于空时编码方法的。
2.1分层空时码结构
D-BLAST结构是採用空时复用技术达到MIMO系统的理论容量的一个方案，由于它的複杂度高不易实现，Bell实验室在1998年将这个体系进行了进一步的改进，提出了V-BLAST的新结构，如图1所示。这种结构比之以前的结构简单了许多，从而便于套用，同时它能达到很高的速率，在复散射、实际的信噪比以及较良性的环境下，它的频谱效率能达到20～40bit/(s·Hz)。
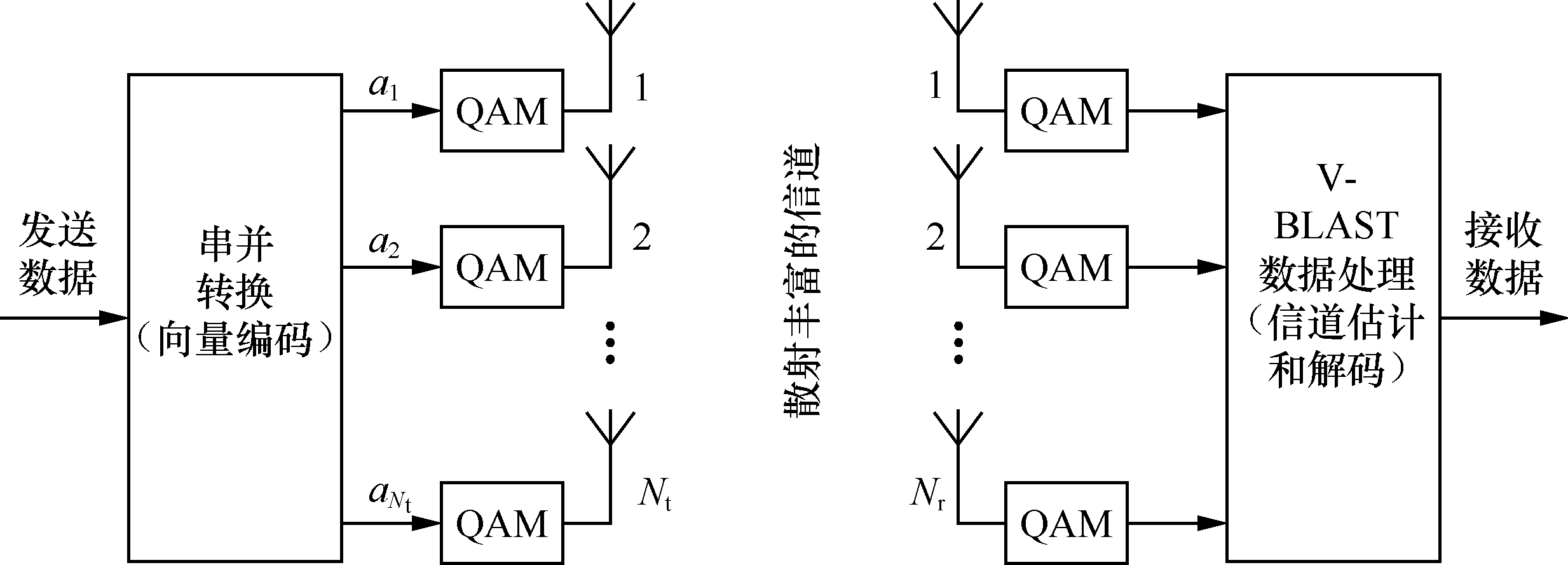
图1V-BLAST结构框图
2.2V-BLAST系统的检测方法
1．最大似然（ML）检测
众所周知，ML检测算法是最优的检测算法，它将接收信号与所有可能的传送信号矢量进行比较，然后依据最大似然原则估计出传送的符号矢量s：
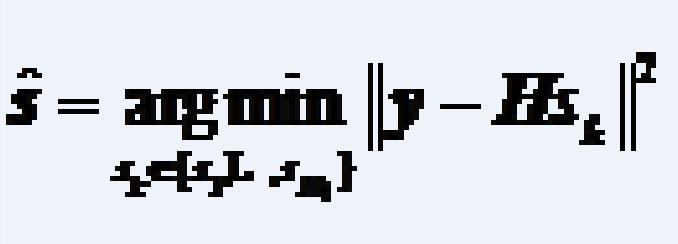
（3.30）
其中s是估计的符号矢量。最大似然检测从所有的信号星座图中寻找具有最大机率的传送信号矢量。然而，由于这种比较複杂度随着传送天线的增加呈指数增加，这在实际中是很难实现的。这是该方法唯一的缺点。
2．迫零检测算法
在ZF检测算法中，选择权重矢量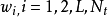
，使满足如下条件：
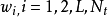
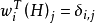
其中(H)j表示H的第j列。那幺第i个子流的判决统计结果为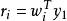
。即wi必须正交于由y的各个未检测分量张成的子空间。
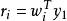
3．MMSE检测算法
4．QR分解检测算法
基于QR分解（QRdecomposition）的检测方法与上述串列干扰对消（SIC）算法本质上是一致的，但QR分解形成的上三角矩阵结构使该算法更为直观，另外这种算法对于分析BLAST的检测性能也很有作用。
QR分解可以将信道矩阵H分解成一个
列正交矩阵Q与一个 三角阵R的乘积[22]，即：
H=Q.R （3.39）
用hi表示信道矩阵H的第i列，qi表示Q的第i列。
分集复用折中
面提到MIMO的两种关键技术：V-BLAST技术和空时分组码（STBC）技术分别具有空间复用增益和空间分集增益，研究表明这两种技术之间存在着此消彼涨的折中关係。本节利用中断公式根据分集增益与多路复用增益之间的折中刻画了慢衰落MIMO信道的性能，之后利用这一折中作为统一框架对本书介绍的各种空时编码方案进行了比较。
3.1标量瑞利信道
1．PAM与QAM
考虑慢衰落标量瑞利信道y=hx+n，其中，加性噪声为独立同分布CN(0,1)随机变数，功率约束等于SNR。假定h服从CN(0,1)分布，考虑採用数据速率为Rbit/(s·Hz)的脉冲幅度调製（PAM）未编码通信。平均差错机率受到PAM星座点之间最小距离的控制，星座的变化範围大约从
到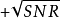
，由于存在2R个星座点，所以最小距离近似为：
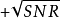
并且高信噪比时的差错机率近似为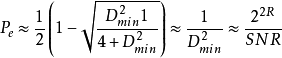
，设数据速率为R=rlgSNR则有
。
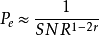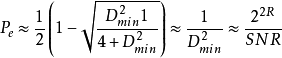
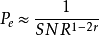
于是得到的分集—多路复用折中为：
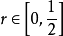
注意，在上述差错机率的近似分析中，关注的是差错机率对信噪比和数据速率变化的比例关係，但忽略了常数乘法器，就分集—多路复用折中而言，它们并不会产生什幺影响。对数据速率为R的QAM可以重複同样的分析，此时在虚实二维各存在2R/2个星座点，因此最小距离近似为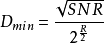
。并且高信噪比时的差错机率近似为
。
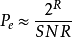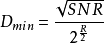
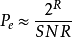
于是得到的分集—多路复用折中为：
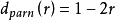
折中曲线如图2所示。
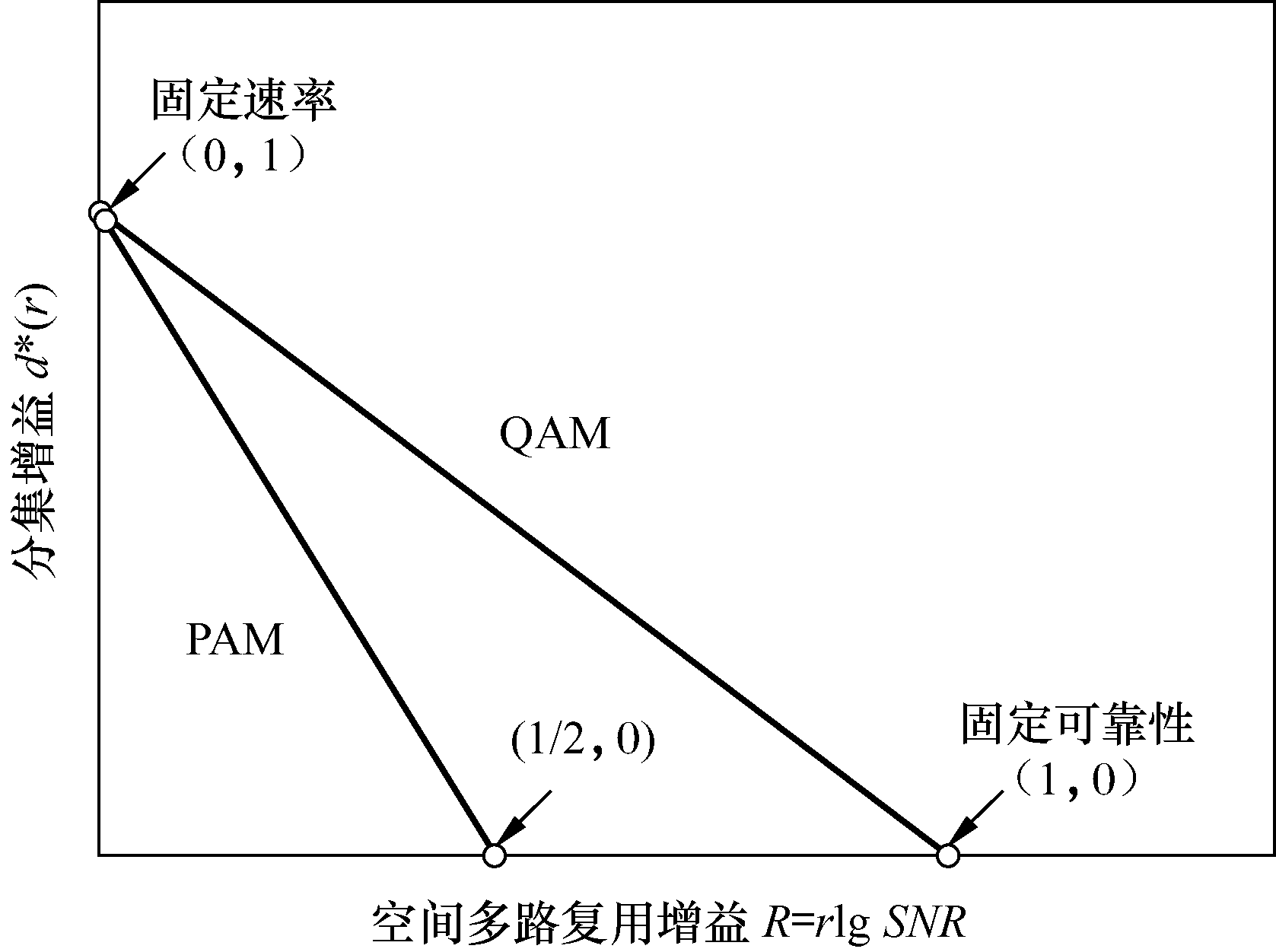
图2单天线慢衰落瑞利信道的折中曲线
2．最优折中
未编码PAM与QAM。标量信道本身的基本分集—多路复用折中如何呢？对于慢衰落瑞利信道而言，目标数据速率R=rlgSNR时的高信噪比中断机率为：
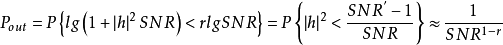
其中，最后一步利用了如下事实，即对于很小的
，在瑞利信道中有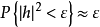
。于是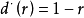
。
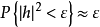
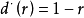
因此，未编码QAM方案实现了分集增益与多路复用增益之间的最优折中。
3.2并行瑞利信道
考虑慢衰落并行信道，其各子信道服从独立同分布瑞利衰落。
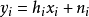
其中，nI为独立同分布CN（0,1）加性噪声，每路子信道的发射功率受到SNR的约束。L路瑞利衰落子信道提供的（经典）分集增益等于L，这就是对基本单天线慢衰落信道的L倍改善。按照前一节介绍的说法，这就是说d*(0)=L。对于任意正的多路复用速率而言，分集增益如何呢？
假定每路子信道的目标数据速率为R=rlgSNR bit/(s gHz)，最优分集d*(r)可以利用终端机率随信噪比增加而减小的速率来计算。对于独立同分布瑞利衰落并行信道而言，每路子信道速率为R=rlgSNR 时的中断机率为：
当各子信道无法支持速率R时，通常会出现中断，可以得到：
因此包括L条分集支路的并行信道的最优分集—多路复用折中为。
即对于每个多路复用增益r，都是标量单天线性能的L倍，这一性能曲线如图3所示。
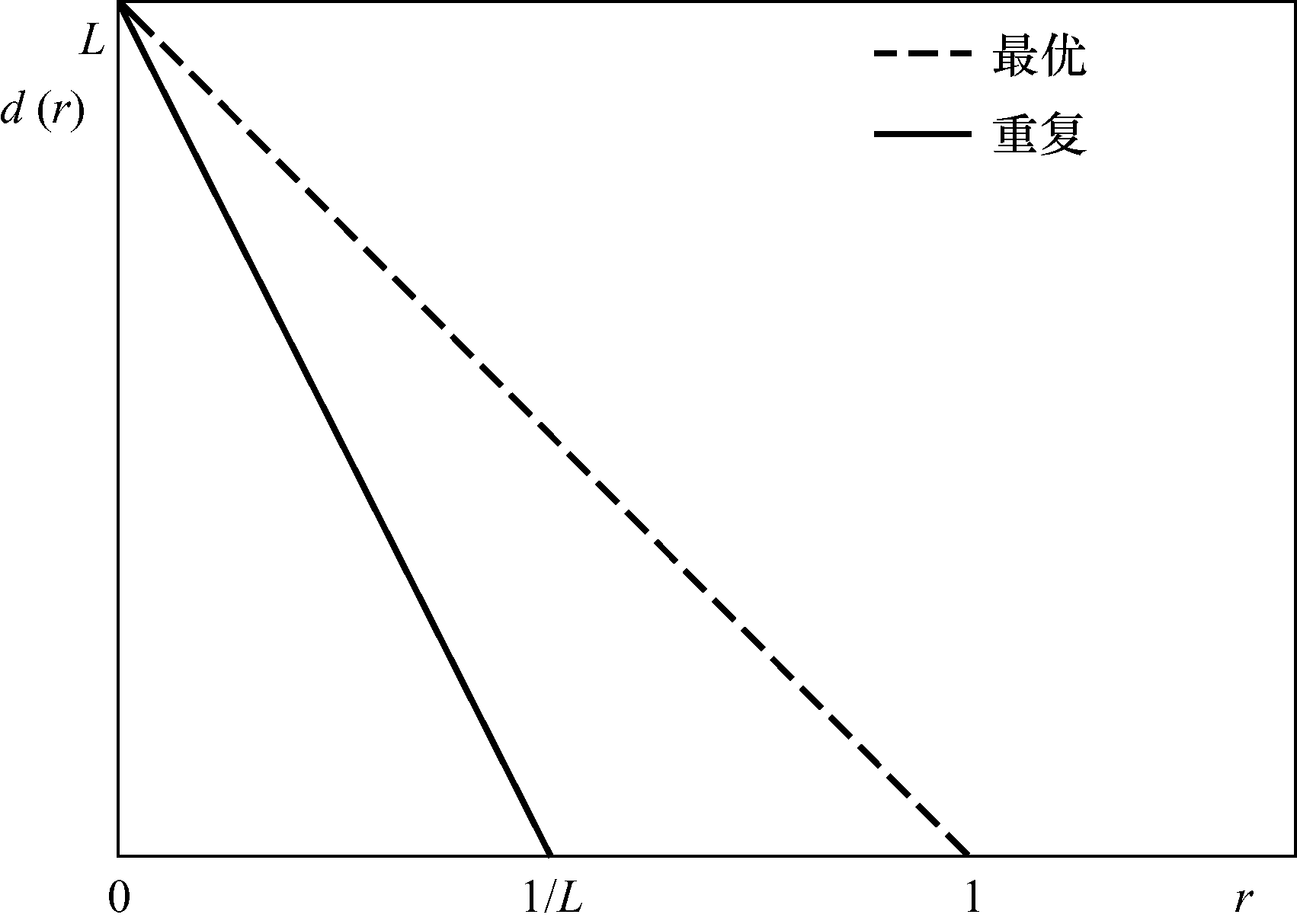
图3包括L路子信道的独立同分布瑞利衰落并行信道以及重複传送方案的分集—多路复用折中
3.3MISO瑞利信道
考虑包括Nt副发射天线与一副接收天线且係数为独立同分布瑞利随机变数的MISO信道：
y=h*s+n （3.54）
与前面一样，加性噪声为独立同分布CN（0,1）随机变数，总的发射功率约束为SNR。我们已经看到包括Nt副发射天线的瑞利衰落的MISO信道提供的（经典）分集增益为Nt。当正的多路复用速率为r时，这一分集增益会增加多少呢？
研究目标数据速率R=rlgSNR bit/(s gHz)时的中断机率就可以回答这个问题：
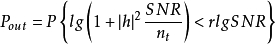
此时|h|2是自由度为2Nt的χ2随机变数，并且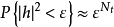
，因此，pout随着信噪比的增大依
规律减小，独立同分布瑞利衰落MISO信道的最优分集—多路复用折中为d*(r)=Nt(1-r) r∈[0,1]。
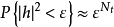
于是，MISO信道在所有多路复用增益时提供的分集增益增大Nt倍。
3.42×2MIMO瑞利信道
对于2×2独立同分布瑞利衰落的MIMO信道中4种方案与未编码QAM结合使用时的分集—多路复用折中，如表1的总结以及图4所示，採用的经典分集增益与自由度对应于图中这些曲线的端点。
表1 经典分级增益与自由度对应关係
经典分集增益 | 所利用的自由度 | 分集—多路复用折中 | |
重複编码 | 4 | 1/2 | 4-8r，r∈[0,1/2] |
Alamouti | 4 | 1 | 4-4r,r∈[0,1] |
V-BLAST（ML） | 2 | 2 | 2-r,r∈[0,2] |
V-BLAST（nulling） | 1 | 2 | 1-r/2,r∈[0,2] |
信道本身 | 4 | 2 | 4-3r,r∈[0,1] 2-r,r∈[1,2] |
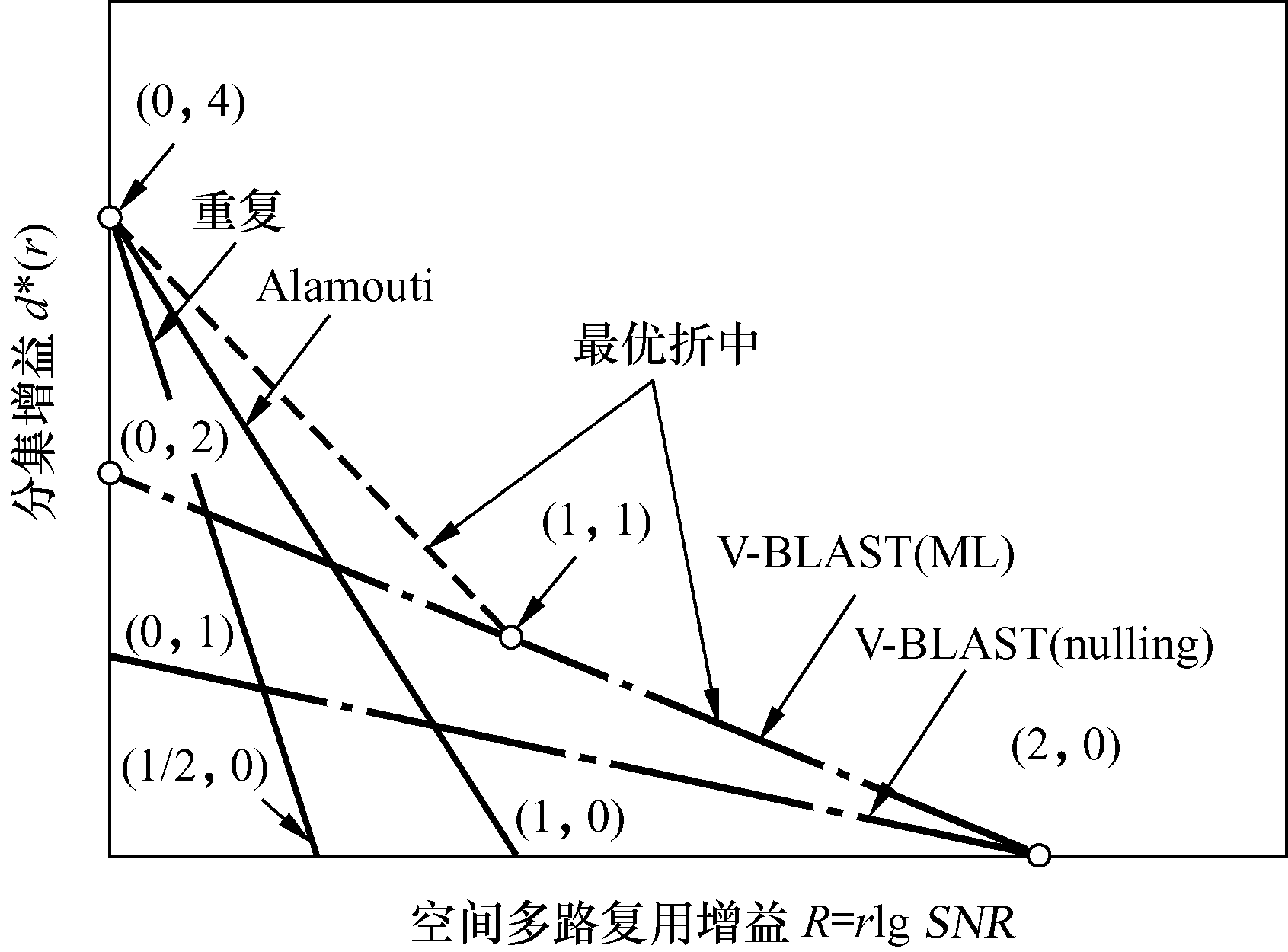
图42×2独立同分布瑞利衰落MIMO信道中4种传送方案的分集—多路复用折中
3.5Nt×NrMIMO瑞利信道
考虑Nt×NMIMO信道独立同分布瑞利衰落增益。数据速率为R=rlgSNR bit/(s gHz)的最优分集增益就是中断机率随SNR减小的速率：
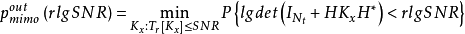
虽然最优协方差矩阵
取决于信噪比和数据速率，通常选择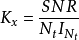
作为实际中断机率的良好近似。在折中曲线公式的粗略比例关係中，这一结论更为準确：式（3.58）中断机率的减小速率与协方差矩阵为单位阵时的情况相同。因此，为了确定多路复用速率为r时的最优分集增益：
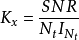
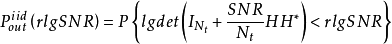
通过分析这个表达式，就可以计算出Nt×Nr独立同分布瑞利衰落信道的分集—多路复用折中，即如图5所示的连线以下各点的分段线性曲线：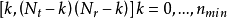
。
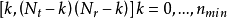
折中曲线简洁地总结了慢衰落MIMO信道的性能。在r→0的一种极端情况下，所实现的最大分集增益Nt×Nr是以极低的多路复用增益为代价的；在r→nmin的另一种极端情况下，可以获得全部自由度。然而系统此时非常接近快衰落容量，几乎不存在对于慢衰落信道随机性的保护，分集增益趋近于0。折中曲线连线着这两个极端，并且提供了比这两个极端点更全面的慢衰落性能图示。例如，系统中增加一副发射天线和一副接收天线就可以使自由度min（Nt，Nr）增加1，这对应于使最大可能的多路复用增益增加1。折中曲线给出了关于系统优势更为精炼的图示：对于任意分集要求d而言，所能够支持的多路复用增益增加1，这是因为这个折中曲线向右平移1。
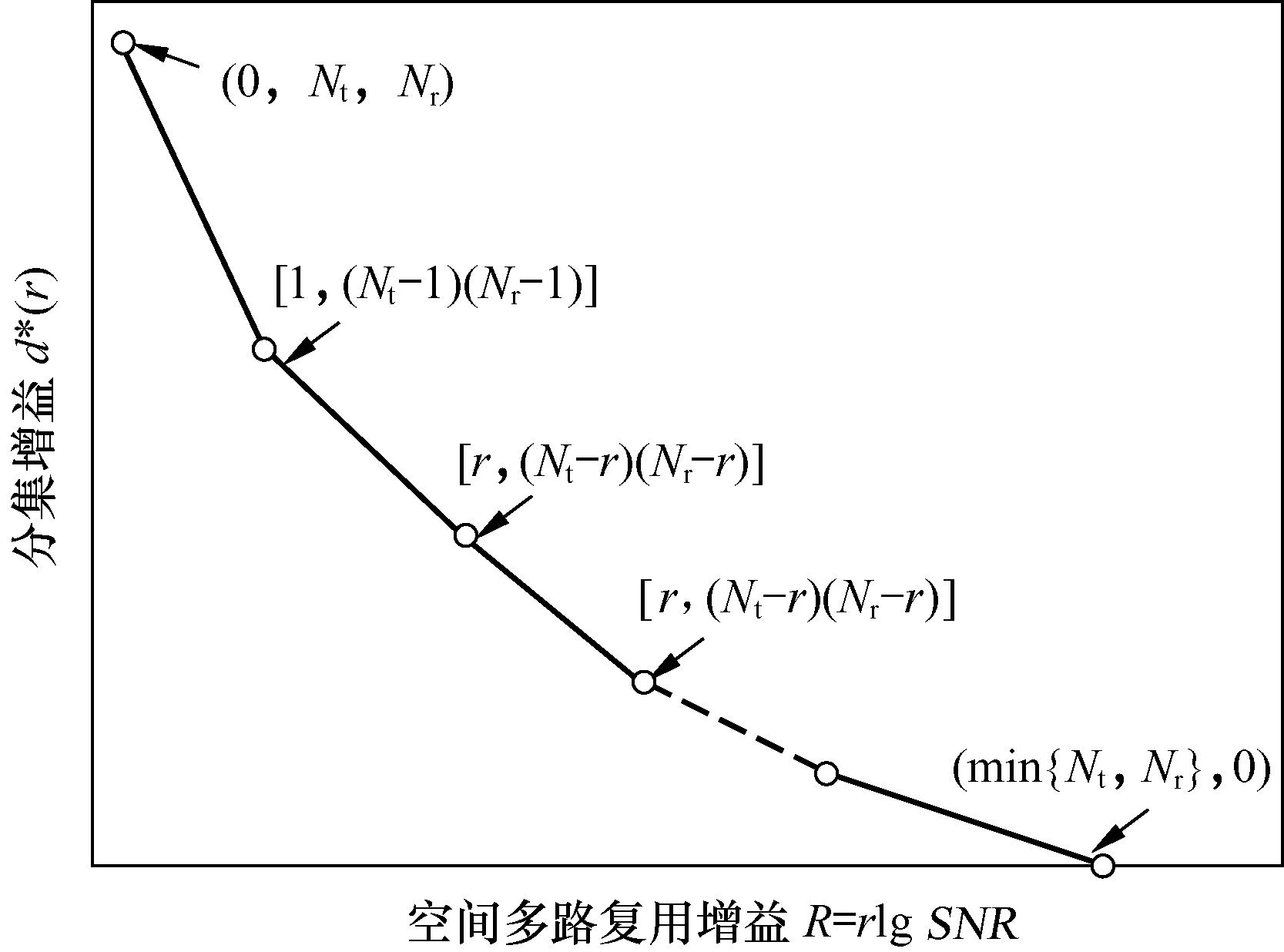
图5独立同分布瑞利衰落信道的分集—多路复用折中
由于最优折中曲线是基于中断机率的，所以要实现最优折中曲线理论上要求分组长度任意大。然而，实际上已经证明分组长度为l=Nt+Nr−1的空时码可以实现这一曲线。