形如y'+P(x)y=Q(x)的微分方程称为一阶线性微分方程，Q(x)称为自由项。一阶，指的是方程中关于Y的导数是一阶导数。线性，指的是方程简化后的每一项关于y、y'的次数为0或1。
基本介绍
- 中文名：一阶线性微分方程
- 外文名：First order linear differential equation
- 定义：形如y'+P(x)y=Q(x)的微分
- 分类：当Q(x)≡0时，方程为y'+P(x)y=0
- 解法：一般用常数变易法
定义
形如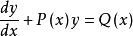
（记为式1）的方程称为一阶线性微分方程。其特点是它关于未知函式y及其一阶导数是一次方程。这里假设
，
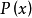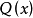是x的连续函式。
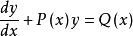
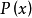
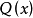
若
，式1变为
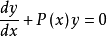（记为式2）称为一阶齐线性方程。
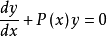
如果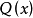不恆为0，式1称为一阶非齐线性方程，式2也称为对应于式1的齐线性方程。
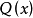
式2是变数分离方程，它的通解为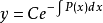
，这里C是任意常数。
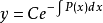
通解求法
一阶线性微分方程的求解一般採用常数变易法，通过常数变易法，可求出一阶线性微分方程的通解。
一阶齐次线性微分方程
对于一阶齐次线性微分方程：
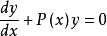
其通解形式为：
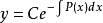
其中C为常数，由函式的初始条件决定。
一阶非齐次线性微分方程
对于一阶非齐次线性微分方程：
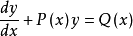
其对应齐次方程: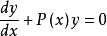 解为：
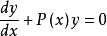
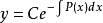
令C=u(x)，得:
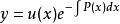
带入原方程得：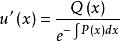
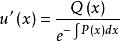
对u’(x)积分得u(x)并带入得其通解形式为：
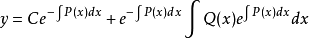
其中C为常数，由函式的初始条件决定。
注意到，上式右端第一项是对应的齐线性方程式（式2）的通解，第二项是非齐线性方程式（式1）的一个特解。由此可知，一阶非齐线性方程的通解等于对应的齐线性方程的通解与非齐线性方程的一个特解之和。